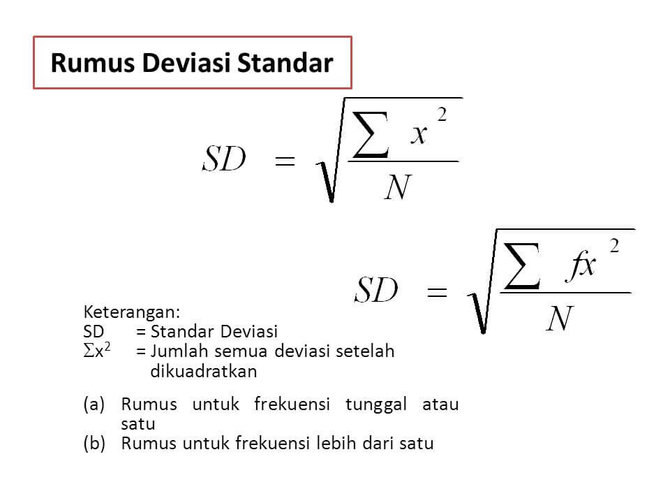
Standar deviasi merupakan salah satu konsep penting dalam statistik yang sering digunakan untuk mengukur seberapa jauh data berbeda dari rata-rata atau mean. Standar deviasi diperhitungkan dengan menggunakan rumus tertentu yang menghitung perbedaan antara setiap data dan rata-rata, kemudian menjumlahkan seluruh perbedaan tersebut dan menghitung rata-rata perbedaan. Perhitungan standar deviasi digunakan dalam berbagai bidang seperti ilmu sosial, ilmu ekonomi, ilmu kesehatan, ilmu pangan, dan masih banyak lagi.
Cara Membuat Grafik Standar Deviasi di Excel
Excel adalah salah satu program komputer yang sering digunakan dalam menghitung dan menganalisis data, termasuk dalam menghitung standar deviasi. Berikut adalah langkah-langkah untuk membuat grafik standar deviasi di Excel:
- Siapkan data yang ingin dihitung standar deviasinya di Excel.
- Buka program Excel dan masukkan data pada kolom atau baris yang tersedia.
- Pilih seluruh kolom atau baris data yang telah dimasukkan.
- Klik pada tab “Insert” di bagian atas dan pilih grafik yang diinginkan, misalnya “Line Chart”.
- Pada grafik yang muncul, klik pada salah satu titik data atau garis grafik.
- Klik kanan pada titik atau garis tersebut dan pilih “Add Trendline” atau “Tambahkan Garis Trend”.
- Pilih opsi “Linear” atau “Linier” pada jendela yang muncul dan centang opsi “Display Equation on Chart” atau “Tampilkan Persamaan pada Grafik”.
- Pilih opsi “R-squared value” atau “Nilai R-kuadrat” dan klik OK.
- Setelah selesai, grafik standar deviasi akan muncul pada layar Excel.
Standar Deviasi Excel
Excel juga menyediakan rumus standar deviasi yang dapat digunakan untuk menghitung standar deviasi dari suatu data. Berikut adalah langkah-langkah untuk menghitung standar deviasi di Excel:
- Buka program Excel dan masukkan data pada kolom atau baris yang tersedia.
- Pilih seluruh kolom atau baris data yang telah dimasukkan.
- Klik pada tab “Formulas” di bagian atas dan cari rumus “STDEV” atau “STDEV.P” pada daftar rumus yang tersedia.
- Klik pada rumus tersebut dan masukkan rentang data yang ingin dihitung standar deviasinya.
- Klik OK dan hasil perhitungan standar deviasi akan muncul pada lembar kerja Excel.
Cara Mencari Standar Deviasi Data Kelompok
Saat menghitung standar deviasi dari data kelompok, rumus yang digunakan berbeda dengan rumus untuk menghitung standar deviasi dari data tunggal. Berikut adalah rumus untuk menghitung standar deviasi dari data kelompok:
Untuk Data dalam rentang tabel:
Standar Deviasi = akar kuadrat[(Ʃf × d²) ÷ (Ʃf) – (Ʃfx)² ÷ (Ʃf)²]
Dengan keterangan:
- f = frekuensi
- x = titik tengah kelas
- d = jarak titik data ke titik tengah kelas
- Ʃf = total frekuensi
- Ʃfx = total perkalian antara frekuensi dan titik tengah kelas
Berikut adalah langkah-langkah untuk menghitung standar deviasi data kelompok:
- Masukkan data kelompok pada kolom pertama excel
- Hitung rentang data dengan mengurangi data terbesar dengan data terkecil dan deviden dengan jumlah data yang diambil
- Hitung titik tengah setiap kelas dengan menjumlahkan titik awal dan akhir kelas, kemudian dibagi 2
- Hitung frekuensi setiap kelas
- Hitung jarak titik data ke titik tengah kelas dengan mengurangkan titik data dengan titik tengah kelas
- Hitung perkalian antara frekuensi dan jarak titik data ke titik tengah kelas untuk setiap kelas
- Hitung total frekuensi dan total perkalian antara frekuensi dan titik tengah kelas
- Masukkan hasil perhitungan pada rumus standar deviasi kelompok yang telah disebutkan di atas
- Setelah selesai, hasil perhitungan standar deviasi kelompok akan muncul pada lembar kerja Excel
+30 Rumus Mencari Standar Deviasi Di Excel References
Untuk memudahkan dalam menghitung standar deviasi di Excel, terdapat beberapa rumus yang dapat digunakan. Berikut adalah beberapa referensi rumus untuk mencari standar deviasi di Excel:
- =STDEV.S(data)
- =STDEV.P(data)
- =STDEVP(data)
- =AVEDEV(data)
- =DEVSQ(data)
- =VAR.P(data)
- =VAR.S(data)
- =VARA(data)
- =STDEVA(data)
- =CONFIDENCE(alpha,standard_dev,size)
- =CRITBINOM(trials,probability_s,alpha)
- =EXPONDIST(x,lambda,cumulative)
- =FDIST(x,degrees_freedom1,degrees_freedom2)
- =FTEST(array1,array2)
- =GAMMADIST(x,alpha,beta,cumulative)
- =LOGEST(known_y’s,[known_x’s],[const],[stats])
- =LOGINV(probability,mean,standard_dev)
- =NORMDIST(x,mean,standard_dev,cumulative)
- =NORMINV(probability,mean,standard_dev)
- =PROB(range,probability,[lower],[upper])
- =TDIST(x,degrees_freedom,tails)
- =VARPA(data)
- =ZTEST(array,μ0,sigma)
- =AVEDEV.S(A1:A10)
- =COVARIANCE.S(range1,range2)
- =COVARIANCE.P(range1,range2)
- =DEV.S(A1:A10)
- =GEOMEAN(A1:A10)
- =HARMEAN(A1:A10)
- =MAX(A1:A10)
FAQ
1. Apa itu standar deviasi?
Standar deviasi adalah suatu ukuran untuk mengukur seberapa jauh data berbeda dari rata-rata atau mean. Standar deviasi digunakan untuk mengetahui seberapa bervariasinya data dan dapat menjadi indikator untuk mengetahui seberapa konsisten data tersebut.
2. Apa perbedaan antara standar deviasi data kelompok dan data tunggal?
Perbedaan antara standar deviasi data kelompok dan data tunggal terletak pada rumus yang digunakan untuk menghitungnya. Rumus standar deviasi data tunggal menghitung perbedaan antara setiap data dan rata-rata, kemudian menjumlahkan seluruh perbedaan tersebut dan menghitung rata-rata perbedaan. Sedangkan, rumus standar deviasi data kelompok menghitung jarak antara titik tengah kelas dan titik data, kemudian mengalikan jarak tersebut dengan frekuensi dan menghitung rata-rata perbedaan.