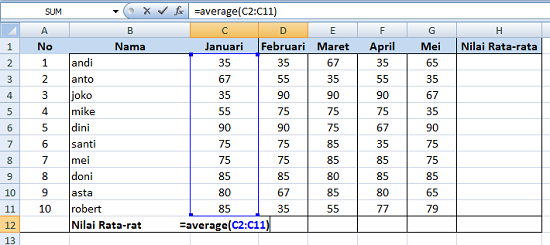
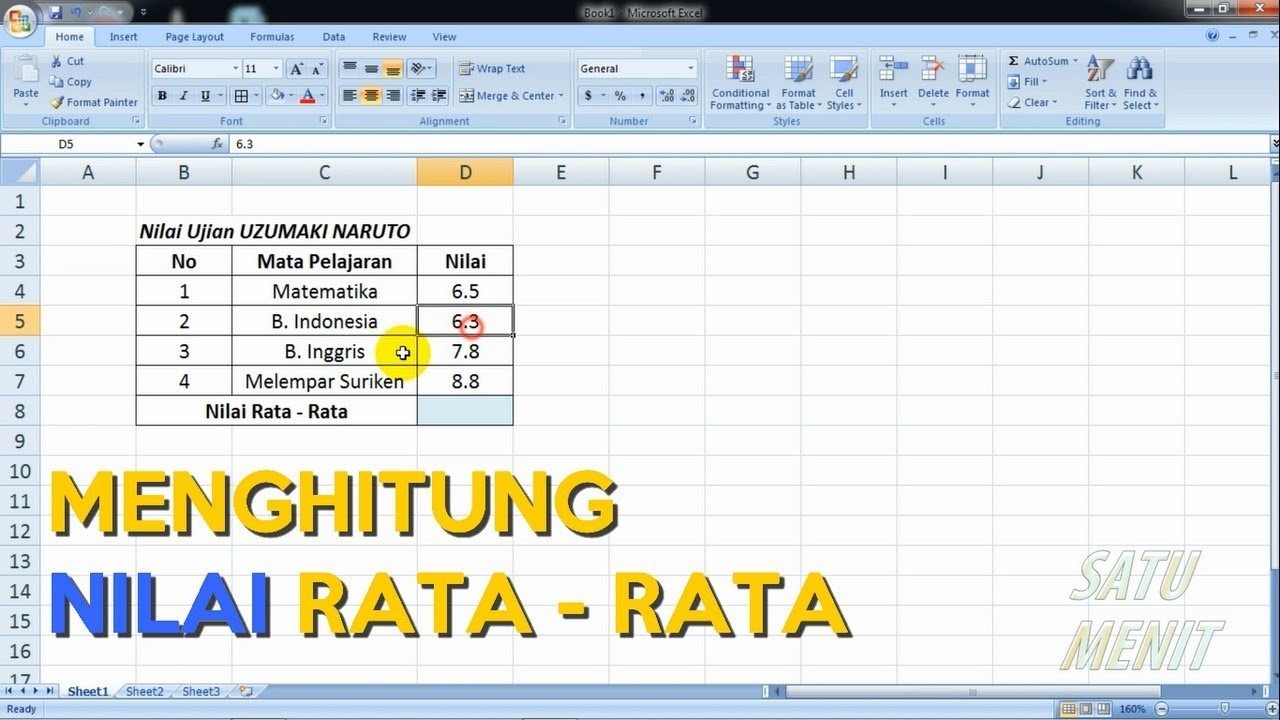
Mengetahui cara menghitung rata-rata merupakan hal penting dalam matematika dan memiliki banyak kegunaan dalam kehidupan sehari-hari. Baik dalam dunia akademik maupun profesionall, menghitung rata-rata dapat membantu dalam pengambilan keputusan, analisis data, dan pemahaman informasi yang ada.
Cara Menghitung Rata-Rata
Ada beberapa metode yang dapat digunakan untuk menghitung rata-rata. Berikut adalah beberapa di antaranya:
1. Rata-rata Aritmatika
Metode paling umum dalam menghitung rata-rata adalah menggunakan rata-rata aritmatika. Rata-rata aritmatika adalah jumlah dari semua nilai yang ada, dibagi dengan jumlah nilai. Untuk n nilai, rata-rata aritmatika dapat dihitung dengan rumus berikut:
Contohnya, bayangkan kita memiliki data nilai dari siswa dalam sebuah ujian matematika:
- 80
- 70
- 90
- 85
Untuk menghitung rata-rata, kita dahulu harus menjumlahkan semua nilai tersebut:
- 80 + 70 + 90 + 85 = 325
Setelah itu, kita bagi dengan jumlah nilai (4) sehingga didapatkan rata-rata:
- 325 ÷ 4 = 81.25
Jadi, rata-rata nilai dari siswa pada ujian matematika tersebut adalah 81.25.
2. Rata-rata Geometrik
Rata-rata geometrik merupakan jenis rata-rata lainnya yang sering digunakan dalam matematika dan statistika. Rata-rata ini digunakan untuk menghitung nilai rata-rata ketika kita memiliki data yang memiliki perbandingan atau rasio. Rumus rata-rata geometrik adalah sebagai berikut:
Contohnya, kita akan menghitung rata-rata geometrik dari data berikut:
- 2
- 4
- 8
Pertama, kita harus mengalikan semua nilai tersebut:
- 2 x 4 x 8 = 64
Kemudian, untuk menghitung rata-rata geometrik, kita ambil akar n dari hasil perkalian tersebut, di mana n adalah jumlah data:
- √(2 x 4 x 8) = √64 = 4
Jadi, rata-rata geometrik dari data di atas adalah 4.
Cara Menghitung Rata-Rata Data Kelompok
Untuk data yang tergolong banyak, terkadang kita membutuhkan cara yang berbeda untuk menghitung rata-rata. Salah satu cara yang dapat digunakan adalah dengan menggunakan rata-rata data kelompok. Rata-rata data kelompok dapat dihitung dengan rumus sebagai berikut:
Contohnya, kita akan menghitung rata-rata dari data kelompok sebagai berikut:
Pertama, kita harus menentukan interval kelas. Interval kelas adalah rentang nilai yang ada dalam suatu kelompok data. Untuk data di atas, interval kelas akan memiliki rentang dari 40-45, 46-50, 51-55, dan seterusnya.
Selanjutnya, kita harus menentukan titik tengah dari masing-masing interval kelas. Titik tengah dihitung dengan menjumlahkan batas bawah dan batas atas interval kelas lalu dibagi dua. Contohnya, titik tengah dari interval kelas 40-45 adalah:
- (40 + 45) ÷ 2 = 42.5
Kita kemudian harus mencatat frekuensi untuk setiap interval kelas. Frekuensi adalah jumlah data yang tergolong dalam suatu interval kelas. Contohnya, dalam data di atas terdapat 3 data yang tergolong dalam interval kelas 40-45.
Dari sini kita dapat menghitung rata-rata data kelompok dengan cara mengikuti rumus yang diberikan sebelumnya:
- Rata-rata = (∑f x t) ÷ ∑f
Di mana f adalah frekuensi dan t adalah titik tengah dari masing-masing interval kelas. Jadi, untuk data di atas, rata-rata dapat dihitung dengan:
- ((3 x 42.5) + (6 x 48) + (8 x 53.5) + (4 x 59) + (1 x 64.5)) ÷ (3 + 6 + 8 + 4 + 1) = 52.8
Jadi, rata-rata dari data kelompok di atas adalah 52.8.
FAQ
1. Apa kegunaan dari menghitung rata-rata?
Menghitung rata-rata dapat memiliki banyak kegunaan, terutama dalam analisis data dan pengambilan keputusan. Misalnya, ketika kita ingin mengetahui kinerja karyawan dalam suatu perusahaan, kita dapat menghitung rata-rata dari nilai-nilai yang mereka peroleh dalam beberapa bulan terakhir untuk mengetahui apakah mereka memenuhi standar atau tidak.
2. Apa perbedaan antara rata-rata aritmatika dan rata-rata geometrik?
Rata-rata aritmatika digunakan untuk menghitung nilai rata-rata ketika kita memiliki data yang tidak memiliki perbandingan atau rasio. Sementara itu, rata-rata geometrik digunakan untuk menghitung nilai rata-rata ketika kita memiliki data yang memiliki perbandingan atau rasio.