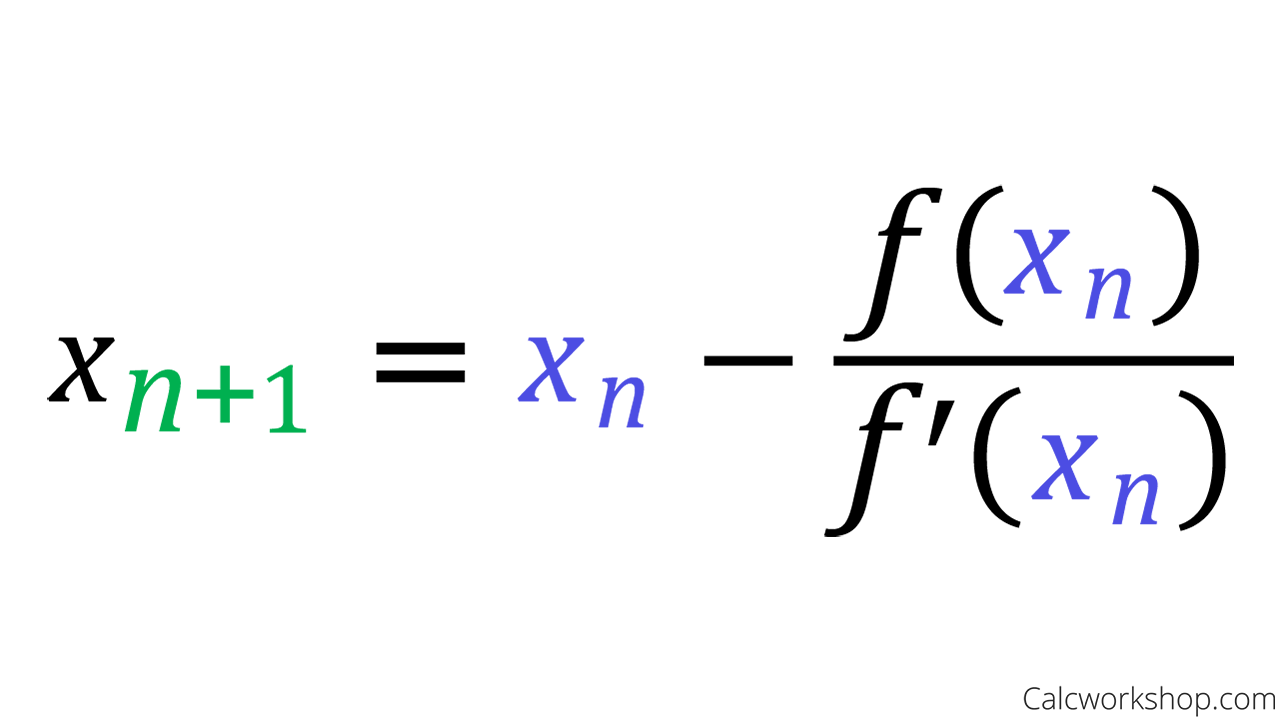Newton’s Method adalah sebuah metode matematika untuk mencari akar suatu persamaan atau fungsi. Metode ini sangat berguna bagi pemecahan masalah yang melibatkan kalkulasi kompleks pada matematika maupun fisika. Dalam dunia akademis, Newton’s Method juga menjadi bagian penting di dalam bidang-bidang seperti teknik dan ilmu komputer.
Perlunya Newton’s Method dalam Pemecahan Masalah
Tidak dapat dipungkiri bahwa matematika adalah sebuah ilmu yang sangat penting bagi kehidupan manusia. Mulai dari penyelesaian masalah keuangan hingga perencanaan konstruksi gedung-gedung megah, semua membutuhkan kalkulasi dalam matematika. Namun, tak jarang kita menemukan masalah kompleks yang tidak bisa diselesaikan hanya dengan alat perhitungan sederhana seperti kalkulator. Itulah mengapa Newton’s Method hadir sebagai salah satu alternatif penting dalam penyelesaian masalah yang melibatkan kalkulasi kompleks.
Cara Kerja Newton’s Method
Cara kerja Newton’s Method cukup sederhana, tetapi membutuhkan pengetahuan matematika yang lebih komprehensif. Secara umum, metode ini bekerja dengan mengambil sebuah tebakan atau nilai awal, kemudian melakukannya iterasi atau pengulangan untuk mendapatkan akar sebenarnya. Pembahasan mengenai detail cara kerja Newton’s Method akan sangat panjang dan abstrak, namun secara umum, prinsipnya adalah mendekati akar sebenarnya dengan teknik turunan dan perhitungan baru.
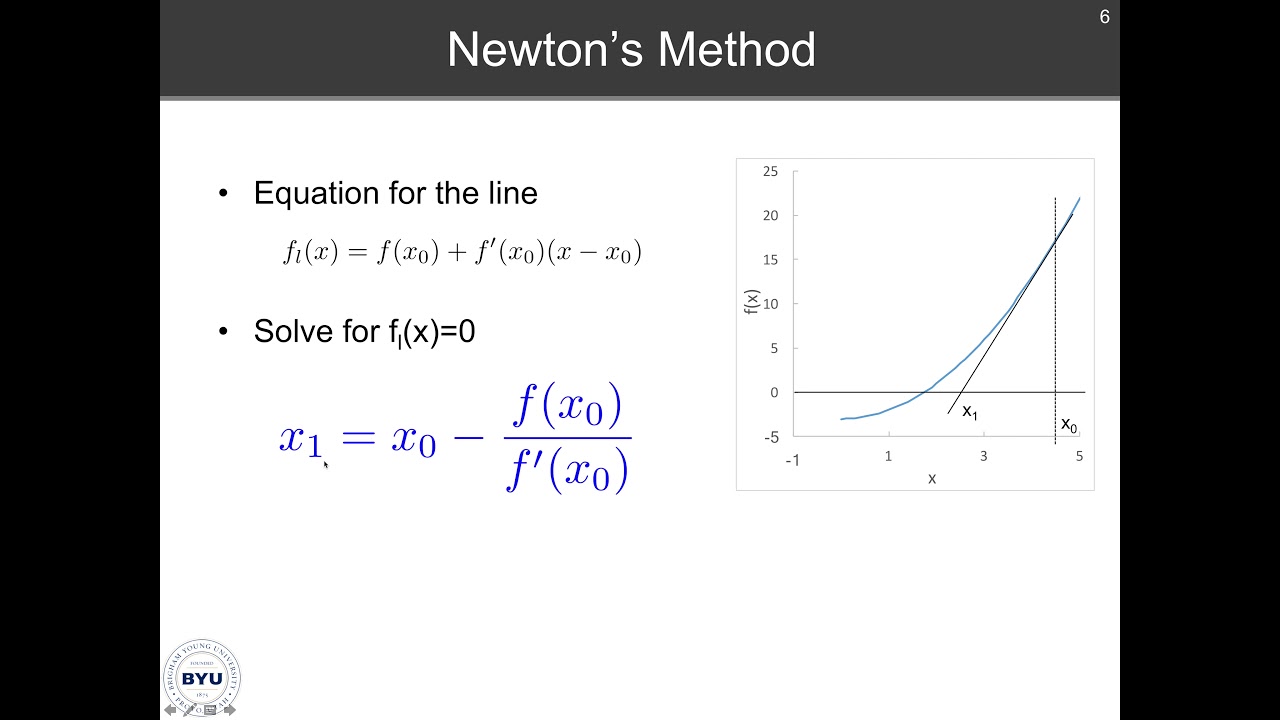
Gambar Ilustrasi Newton’s Method
Gambar ilustrasi di atas menunjukkan bagaimana Newton’s Method bekerja dalam mencari akar suatu persamaan atau fungsi secara numerik. Cara kerjanya memang terlihat kompleks, tetapi dengan memahami prinsip-prinsip matematika yang mendasar, semua itu bisa dilakukan dengan mudah.
FAQ: Pertanyaan Umum mengenai Newton’s Method
Pertanyaan 1: Apa saja kelebihan Newton’s Method?
Jawaban: Salah satu kelebihan utama Newton’s Method adalah kecepatan dalam memberikan hasil akhir. Jika dibandingkan dengan metode-metode lain seperti Bisection Method, Newton’s Method memiliki kemampuan untuk mendekati akar sebenarnya dengan lebih cepat. Selain itu, Newton’s Method juga dapat digunakan untuk menyelesaikan berbagai masalah yang tidak mungkin diselesaikan dengan metode lain, seperti penyelesaian persamaan yang melibatkan bilangan kompleks.
Pertanyaan 2: Apa saja kelemahan Newton’s Method?
Jawaban: Meski Newton’s Method memiliki banyak kelebihan, tetapi tidak akan lengkap jika tidak membahas kelemahannya. Salah satu kelemahan utamanya adalah sensitivitas terhadap nilai awal atau tebakan. Apabila kita menggunakan tebakan yang kurang tepat, maka iterasi yang dihasilkan bisa saja tidak mendekati akar sebenarnya. Selain itu, Newton’s Method juga tidak dapat digunakan pada beberapa tipe persamaan yang tidak memiliki turunan.
Contoh Penerapan Newton’s Method dalam Excel
Seperti yang telah disebutkan sebelumnya, Newton’s Method dapat digunakan dalam berbagai bidang seperti fisika, matematika, dan teknik. Salah satu aplikasi praktis dari metode ini adalah pada software spreadsheet seperti Excel. Berikut ini adalah contoh penerapan Newton’s Method dalam Excel:
1. Menghitung Akar Persamaan Non-Linear
Contoh di atas menunjukkan bagaimana cara menghitung akar suatu fungsi non-linear dengan menggunakan Newton’s Method dalam Excel. Langkah pertama adalah memasukkan tebakan awal di dalam sell A2. Selanjutnya, kita harus menentukan fungsi dari persamaan non-linear yang ingin dihitung akarnya. Pada contoh di atas, fungsi yang digunakan adalah f(x) = x^3 – 2x^2 – 5x + 6. Kemudian, kita perlu menentukan turunan dari fungsi tersebut, yang pada contoh di atas adalah f'(x) = 3x^2 – 4x – 5. Setelah menentukan kedua fungsi tersebut, kita dapat memasukkan rumus Newton’s Method di dalam sell B2 dengan menggunakan rumus =A2-f(A2)/f'(A2). Rumus tersebut akan menghasilkan nilai baru yang merupakan iterasi akar dari persamaan non-linear tersebut. Selanjutnya, kita dapat melakukan iterasi baru dengan memasukkan rumus di dalam sell B3 dengan menggunakan rumus =B2-f(B2)/f'(B2) dan seterusnya hingga ditemukan sebuah nilai yang konvergen atau mendekati akar sebenarnya.
Video Tutorial Newton’s Method
Bagi Anda yang ingin lebih memahami cara kerja Newton’s Method, Anda dapat menonton video tutorial di bawah ini yang akan mengajarkan langkah-langkah praktis dalam penerapan metode ini:
Contoh Penerapan Newton’s Method dalam Kehidupan Sehari-hari
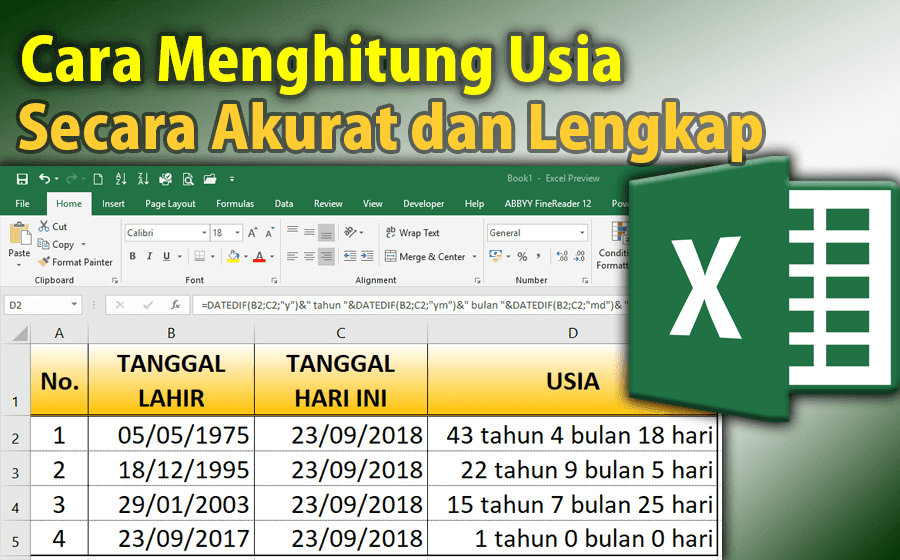
Tidak hanya di bidang akademis, Newton’s Method juga bisa diterapkan dalam kehidupan sehari-hari. Contoh penerapannya adalah pada perhitungan usia seseorang dengan akurat menggunakan Excel. Seperti yang kita ketahui, perhitungan usia merupakan hal yang sangat penting di dalam dunia medis maupun bisnis. Namun, terkadang perhitungan usia yang dilakukan secara manual bisa jadi kurang akurat karena berbagai faktor seperti kesalahan ketik atau penghitungan yang salah.
Contoh di atas menunjukkan bagaimana cara menghitung usia seseorang secara akurat dengan menggunakan Excel. Dalam contoh tersebut, kita perlu menentukan tanggal lahir dan hari ini terlebih dahulu di dalam sell A1 dan B1. Selanjutnya, kita perlu menghitung selisih antara hari ini dan tanggal lahir, yakni dengan menggunakan rumus =YEARFRAC(A1,B1). Kemudian, kita dapat menggunakan Newton’s Method untuk menghitung akar dari persamaan tersebut, di mana f(x) = (todaydate – birthdate)/(365.25/x) – x. Fungsi tersebut akan menghasilkan sebuah nilai iterasi yang konvergen atau mendekati akar sebenarnya, yakni umur seseorang dengan akurat.
Conclusion
Newton’s Method memang bukanlah metode yang mudah dipahami bagi orang awam, tetapi sangat berguna dalam mencari akar suatu persamaan atau fungsi dalam kalkulasi matematika maupun fisika. Dalam dunia akademis, Newton’s Method merupakan salah satu komponen penting di dalam bidang-bidang seperti teknik maupun ilmu komputer. Dalam kehidupan sehari-hari, Newton’s Method juga bisa diterapkan dalam berbagai situasi, seperti pada perhitungan usia seseorang secara akurat dengan menggunakan Excel. Meskipun memiliki beberapa kelemahan, Newton’s Method tetap menjadi alternatif yang paling efektif dalam menyelesaikan masalah yang melibatkan kalkulasi kompleks.