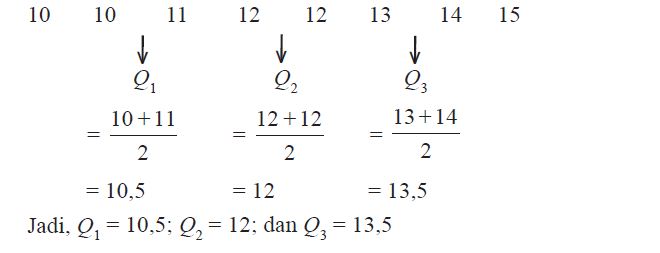Pengetahuan statistik merupakan hal yang penting untuk dipelajari karena dapat membantu dalam mengambil keputusan yang tepat berdasarkan data yang ada. Salah satu konsep penting dalam statistik adalah kuartil, yang digunakan untuk melihat sebaran data dalam sebuah sampel atau populasi.
Rumus Mencari Nilai Tengah – Tulisan Bermakna
Salah satu cara untuk menghitung kuartil adalah dengan menggunakan rumus mencari nilai tengah. Rumus ini dapat digunakan untuk menemukan kuartil atas, median, dan kuartil bawah pada suatu data. Berikut adalah rumusnya:
Kuartil 1 (Q1) = n + 1 / 4
Kuartil 2 (Q2) = n + 1 / 2
Kuartil 3 (Q3) = 3n + 1 / 4
Dimana n adalah jumlah data yang ada dalam sampel atau populasi.
Contoh:
Untuk data diatas, terdapat 11 angka. Dengan mengisi nilai n tersebut dalam rumus diatas kita dapat mencari nilai tengahnya.
Q1 = (11 + 1) / 4 = 3
Q2 = (11 + 1) / 2 = 6
Q3 = (11 x 3 + 1) / 4 = 9
Dengan begitu kita dapat mengetahui bahwa kuartil 1 adalah angka 2, kuartil 2 adalah angka 4.5, dan kuartil 3 adalah angka 7.
Cara Mencari Kuartil Data Kelompok – iFaWorldCup.com
Selain kuartil pada data tunggal, kuartil juga dapat dihitung pada data kelompok. Jika terdapat data kelompok, untuk menghitung kuartil dapat menggunakan rumus sebagai berikut:
Kuartil 1 (Q1) = L + (n/4 – F) x i
Kuartil 2 (Q2) = L + (n/2 – F) x i
Kuartil 3 (Q3) = L + (3n/4 – F) x i
Dimana:
- L adalah batas bawah kelas tempat kuartil berada
- n adalah jumlah data
- F adalah frekuensi kumulatif yang tepat di bawah kuartil yang dicari
- i adalah panjang interval kelas dalam data
Contoh:
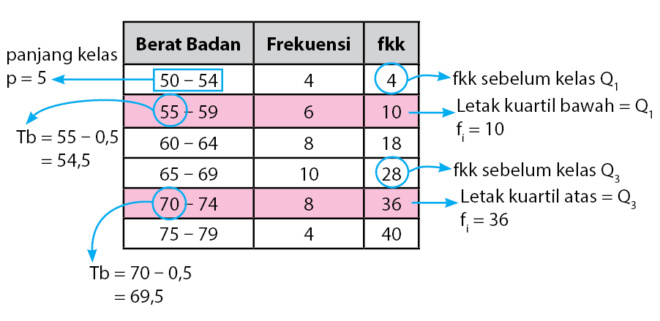
Jika terdapat data kelompok seperti pada gambar diatas, untuk mencari kuartil kita harus menghitung beberapa hal, seperti nilai L, F, dan i terlebih dahulu.
Langkah-langkahnya sebagai berikut:
- Menentukan panjang interval kelas (i) yang diberikan. Pada contoh diatas, i adalah 10.
- Menentukan nilai klas bawah (L) yang diberikan. Dalam contoh diatas, nilai L adalah 40.
- Menentukan frekuensi kumulatif (CF) untuk setiap kelas.
- Mencari nilai F (frekuensi kumulatif) ketika n/4 dan 3n/4 pada tabel frekuensi.
- Jika nilai n/4 dan 3n/4 tidak berada dalam kelas yang sama, maka harus dicari batas atas dan batas bawah untuk mendapatkan frekuensi yang tepat.
Dari hasil perhitungan, didapatkan nilai kuartil sebagai berikut:
Q1 = 50 + (15/4 – 8) x 10 = 62.5
Q2 = 50 + (15/2 – 8) x 10 = 70
Q3 = 50 + (45/4 – 8) x 10 = 85
Cara Cepat Menghitung Median Data Kelompok
Selain kuartil, median juga merupakan salah satu ukuran sebaran data yang sering digunakan dalam statistik. Median adalah nilai tengah dari sebuah data. Untuk menghitung median pada data kelompok, kita dapat menggunakan rumus sebagai berikut:
Median = L + (n/2 – F) x i
Dimana:
- L adalah batas bawah kelas tempat median berada
- n adalah jumlah data
- F adalah frekuensi kumulatif yang tepat di bawah nilai median
- i adalah panjang interval kelas dalam data
Contoh:
Jika terdapat data kelompok seperti pada gambar diatas, untuk mencari median kita harus menghitung beberapa hal, seperti nilai L, F, dan i terlebih dahulu.
Langkah-langkahnya sebagai berikut:
- Menentukan panjang interval kelas (i) yang diberikan. Pada contoh diatas, i adalah 10.
- Menentukan nilai klas bawah (L) yang diberikan. Dalam contoh diatas, nilai L adalah 40.
- Menentukan frekuensi kumulatif (CF) untuk setiap kelas.
- Mencari nilai F (frekuensi kumulatif) ketika n/2 pada tabel frekuensi.
- Jika nilai n/2 tidak berada dalam kelas yang sama, maka harus dicari batas atas dan batas bawah untuk mendapatkan frekuensi yang tepat.
Dari hasil perhitungan, didapatkan nilai median sebagai berikut:
Median = 50 + (20/2 – 10) x 10 = 60
Cara Menghitung Kuartil Bawah, Tengah, dan Atas | idschool
Sebagai seorang ahli data, kita harus mengetahui cara menghitung kuartil bawah, tengah, dan atas pada data kelompok. Kuartil bawah, tengah, dan atas sangat penting untuk mengetahui sebaran data yang ada pada sampel atau populasi. Cara menghitungnya adalah sebagai berikut:
Kuartil Bawah (Q1) = L + [(n/4 – F) x i]
Kuartil Tengah (Q2) = L + [(n/2 – F) x i]
Kuartil Atas (Q3) = L + [(3n/4 – F) x i]
Dimana:
- L adalah batas bawah kelas tempat kuartil berada
- n adalah jumlah data
- F adalah frekuensi kumulatif yang tepat di bawah kuartil yang dicari
- i adalah panjang interval kelas dalam data
Contoh:
Pada contoh di atas, kita dapat melihat data yang terbagi dalam beberapa kelompok, dengan nilai kelas bawah masing-masing kelompok (L) adalah 0, 5, 10, 15, dan 20. Data yang dihitung dari kelompok tersebut juga memiliki panjang interval (i) sebesar 5.
Dari gambar tersebut, kita dapat mengetahui bahwa:
- Jumlah data (n) adalah 20
- Kita perlu mencari nilai frekuensi kumulatif (F) ketika n/4, n/2, dan 3n/4.
Dengan mengikuti rumus di atas, kita akan mendapatkan hasil sebagai berikut:
Kuartil Bawah (Q1) = 5 + [(20 / 4 – 4) x 5] = 10
Kuartil Tengah (Q2) = 5 + [(20 / 2 – 9) x 5] = 15
Kuartil Atas (Q3) = 5 + [(60 / 4 – 9) x 5] = 20
FAQ
1. Mengapa kuartil penting dalam statistik?
Kuartil digunakan untuk melihat sebaran data dalam sebuah sampel atau populasi. Dengan mengetahui kuartil pada suatu data, kita dapat mengetahui distribusi data tersebut, apakah memiliki sebaran yang merata atau tidak. Selain itu, kuartil juga dapat digunakan untuk menghitung interquartile range (jarak antarkuartil), yang mana dapat digunakan untuk menentukan outliers pada suatu data.
2. Apa bedanya kuartil pada data tunggal dan data kelompok?
Kuartil pada data tunggal merupakan kuartil yang digunakan untuk menghitung distribusi data tunggal, sedangkan kuartil pada data kelompok digunakan untuk menghitung distribusi data pada kelompok yang dibagi dalam interval kelas. Untuk menghitung kuartil pada data tunggal, kita hanya perlu mencari nilai tengah dari data, sedangkan untuk menghitung kuartil pada data kelompok kita perlu menghitung beberapa hal, seperti nilai L, F, dan i terlebih dahulu.
Video Tutorial
Demikianlah pembahasan mengenai kuartil pada data tunggal dan data kelompok. Dengan memahami konsep kuartil, kita dapat menggunakan informasi tersebut untuk mengambil keputusan yang lebih tepat berdasarkan data yang ada.