Berikut ini adalah beberapa gambar dan penjelasannya tentang standar deviasi, mulai dari cara menghitung rata-rata berat badan tabel hingga fungsi standar deviasi dan perhitungannya. Selain itu, juga akan dibahas cara menentukan mean, median, modus, dan standar deviasi serta rata-rata data kelompok dengan interval kelas. Yuk, simak penjelasannya!
Cara Menghitung Rata-Rata Berat Badan Tabel
Rata-rata berat badan adalah nilai tengah dari suatu kelompok atau populasi data yang terdiri dari berat badan individu. Cara menghitung rata-rata berat badan dari tabel adalah sebagai berikut:
- Menjumlahkan semua nilai berat badan pada kolom yang ada pada tabel.
- Memperoleh jumlah data yang ada pada kolom tersebut.
- Membagi hasil penjumlahan tersebut dengan jumlah data pada kolom tersebut.
Contoh:
| Jenis Kelamin | Berat Badan (kg) |
|---|---|
| Laki-laki | 60 |
| Perempuan | 50 |
| Laki-laki | 65 |
| Perempuan | 55 |
Jadi, rata-rata berat badannya adalah:
(60 + 50 + 65 + 55) / 4 = 57,5 kg
Fungsi Standar Deviasi dan Perhitungannya
Standar deviasi adalah suatu ukuran untuk mengetahui seberapa bervariasi data dalam kelompok atau populasi. Fungsi standar deviasi meliputi:
- Mengetahui seberapa jauh data berada dari nilai rata-ratanya.
- Mengetahui distribusi data dalam kelompok atau populasi.
- Mengetahui seberapa akurat nilai rata-rata dalam merepresentasikan kelompok atau populasi.
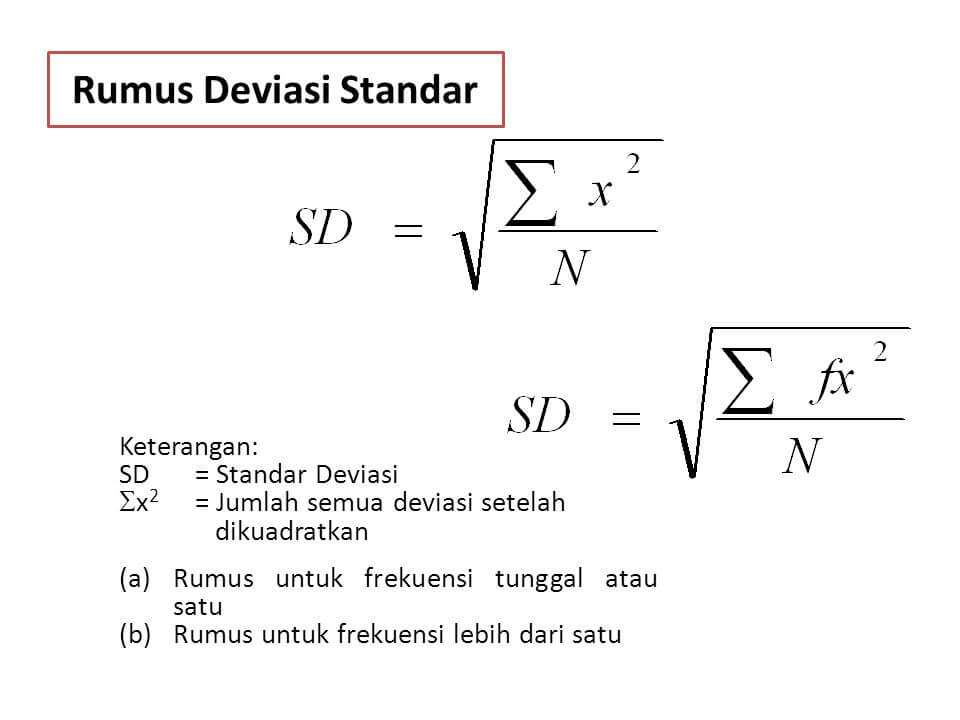
Rumus standar deviasi adalah:
Contoh:
| No | Nilai |  |
 |
 |
|---|---|---|---|---|
| 1 | 80 | 6400 | 16 | 256 |
| 2 | 75 | 5625 | -5 | 25 |
| 3 | 90 | 8100 | 10 | 100 |
| 4 | 82 | 6724 | 2 | 4 |
| 5 | 78 | 6084 | -2 | 4 |
| 6 | 85 | 7225 | 5 | 25 |
| Σ | 490 | 40058 | 26 | 414 |
Jadi, standar deviasinya adalah:
Cara Menentukan Mean (Rata-rata), Median, Modus, dan Standar Deviasi
Mean (rata-rata), median, dan modus adalah tiga jenis angka yang digunakan dalam statistik untuk mewakili kelompok data. Rata-rata adalah jumlah semua angka dalam kelompok data, dibagi dengan jumlah angka tersebut. Median adalah angka tengah dalam kelompok data, sedangkan modus adalah angka yang paling sering muncul dalam kelompok data. Cara menentukan mean, median, dan modus adalah sebagai berikut:
- Urutkan data dari nilai terkecil ke nilai terbesar.
- Hitung mean dengan menjumlahkan semua angka dalam kelompok data, lalu dibagi dengan jumlah angka tersebut.
- Hitung median dengan menentukan angka tengah dalam kelompok data. Jika jumlah angka dalam kelompok data ganjil, maka median adalah angka tengah. Jika jumlah angka dalam kelompok data genap, maka median adalah rata-rata dari dua angka tengah.
- Hitung modus dengan menentukan angka yang paling sering muncul dalam kelompok data. Jika hanya ada satu angka yang paling sering muncul, maka angka tersebut adalah modus. Jika ada lebih dari satu angka yang paling sering muncul, maka kelompok data tersebut tidak memiliki modus tunggal.
Contoh:
| No | Nilai |
|---|---|
| 1 | 60 |
| 2 | 56 |
| 3 | 62 |
| 4 | 58 |
| 5 | 64 |
| 6 | 50 |
| 7 | 66 |
| 8 | 52 |
| 9 | 68 |
| 10 | 54 |
| Σ | 580 |
Jadi, mean (rata-rata) dari kelompok data tersebut adalah:
580 / 10 = 58
Jumlah angka dalam kelompok data adalah genap, yaitu 10. Oleh karena itu, median adalah rata-rata dari dua angka tengah, yaitu:
(56 + 58) / 2 = 57
Modus dari kelompok data tersebut adalah angka yang paling sering muncul, yaitu:
Tidak ada modus tunggal, karena setiap angka muncul hanya satu kali.
Untuk menghitung standar deviasi dari kelompok data tersebut, dapat menggunakan rumus standar deviasi seperti pada subbab sebelumnya.
Rata-Rata Data Kelompok dengan Interval Kelas
Ketika data telah dikelompokkan dengan suatu rentang atau interval tertentu, maka untuk menghitung rata-rata data tersebut harus digunakan metode rata-rata data kelompok dengan interval kelas. Cara menghitungnya adalah sebagai berikut:
- Menentukan titik tengah untuk setiap interval kelas.
- Menjumlahkan (titik tengah x frekuensi) untuk semua interval kelas.
- Memperoleh jumlah semua frekuensi.
- Membagi hasil penjumlahan (titik tengah x frekuensi) dengan jumlah semua frekuensi.
Contoh:
| Interval Kelas | Frekuensi | Titik Tengah | Titik Tengah x Frekuensi |
|---|---|---|---|
| 10 – 20 | 5 | 15 | 75 |
| 20 – 30 | 10 | 25 | 250 |
| 30 – 40 | 20 | 35 | 700 |
| 40 – 50 | 15 | 45 | 675 |
| Σ | 50 | – | 1700 |
Jadi, rata-rata data kelompok tersebut adalah:
1700 / 50 = 34
FAQ
Berikut adalah beberapa pertanyaan yang sering ditanyakan tentang standar deviasi:
1. Apa yang dimaksud dengan standar deviasi?
Standar deviasi adalah suatu ukuran untuk mengetahui seberapa bervariasi data dalam kelompok atau populasi.
2. Apa fungsi dari standar deviasi?
Fungsi standar deviasi meliputi:
- Mengetahui seberapa jauh data berada dari nilai rata-ratanya.
- Mengetahui distribusi data dalam kelompok atau populasi.
- Mengetahui seberapa akurat nilai rata-rata dalam merepresentasikan kelompok atau populasi.
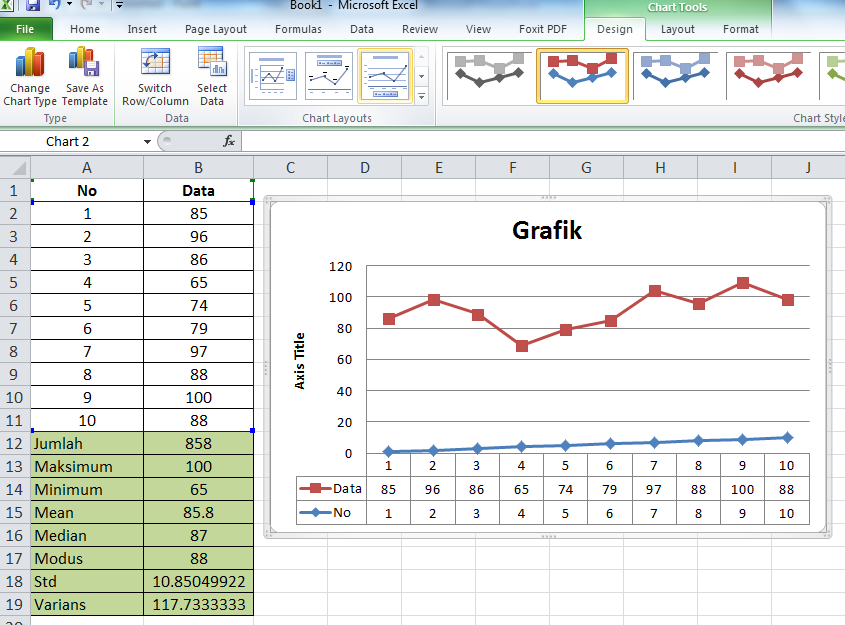
Video Tutorial – Menghitung Deviasi Rata-Rata
Berikut adalah video tutorial yang menjelaskan cara menghitung deviasi rata-rata menggunakan Excel.