Banyak cara yang dapat digunakan untuk menganalisis data, salah satunya adalah dengan menggunakan kuartil. Kuartil adalah suatu nilai yang membagi data yang telah diurutkan menjadi empat bagian yang sama besarnya. Misalnya, jika sebuah data terdiri dari 25 nilai, maka setiap kuartil akan membagi data tersebut menjadi 6 nilai. Kuartil dapat membantu dalam menganalisis data dan memperoleh informasi yang lebih rinci tentang data. Berikut ini akan dijelaskan tentang Simpangan Kuartil, Cara Menghitung Kuartil, Contoh Soal Kuartil, dan Faq Kuartil.
Simpangan Kuartil
Simpangan kuartil adalah jarak antara kuartil bawah dan kuartil atas. Simpangan kuartil digunakan untuk mengukur seberapa besar sebaran data. Semakin besar simpangan kuartil, maka sebaran datanya juga semakin besar. Sedangkan, semakin kecil simpangan kuartil, maka sebaran data juga semakin kecil. Simpangan kuartil dapat digunakan dalam berbagai jenis data, baik data tunggal maupun data kelompok.
Cara Menghitung Kuartil
Untuk menghitung kuartil, terlebih dahulu harus diurutkan data secara berurutan, kemudian dihitung median atau kuartil kedua (Q2). Median adalah nilai tengah dari data yang telah diurutkan. Setelah median diketahui, maka data dipecah menjadi dua bagian, yaitu bagian kiri dan bagian kanan dari median. Kemudian, dihitung nilai median atau kuartil pertama (Q1) untuk bagian kiri dan kuartil ketiga (Q3) untuk bagian kanan dari median.
Rumus kuartil adalah :
Di dalam rumus tersebut, L adalah nilai yang menjadikan data masuk ke dalam kuartil, n adalah banyaknya data, F adalah frekuensi kumulatif hingga nilai L, dan C adalah frekuensi kelas sebelum kelas tempat nilai L masuk.
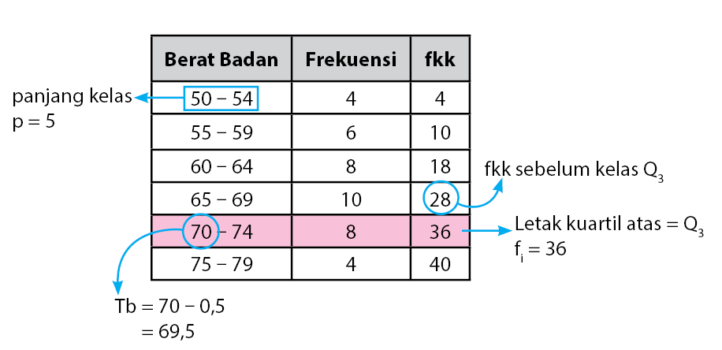
Cara Menghitung Kuartil pada Data Kelompok
Untuk menghitung kuartil pada data kelompok, terlebih dahulu data harus dipecah menjadi kelas dengan interval tertentu. Kemudian, nilai median atau kuartil kedua dihitung dengan rumus :
Median = L + (n/2 – F) / f x i
Setelah median diketahui, maka dihitung kuartil pertama dan kuartil ketiga dengan rumus :
Q1 = L + (n/4 – F) / f x i
Q3 = L + (3n/4 – F) / f x i
Cara Menghitung Kuartil pada Data Tunggal
Untuk menghitung kuartil pada data tunggal, caranya lebih mudah karena hanya perlu mengurutkan data secara berurutan dan mencari nilai median atau kuartil kedua. Setelah median diketahui, kuartil pertama dan kuartil ketiga dapat dihitung dengan cara yang sama seperti pada data kelompok.
Contoh Soal Kuartil
Berikut adalah contoh soal kuartil untuk data tunggal dan data kelompok beserta pembahasannya.
Contoh Soal 1
Berikut adalah data tinggi badan siswa SMP : 160, 165, 155, 170, 175, 155, 160, 165, 170, 160. Hitunglah kuartil pertama, kuartil kedua, dan kuartil ketiga.
Pembahasan
Langkah pertama adalah mengurutkan data yang diberikan :
155, 155, 160, 160, 160, 165, 165, 170, 170, 175
Karena terdapat 10 data, nilai median atau kuartil kedua akan sama dengan nilai ke-5 (nilai tengah) dan 10/2 = 5. Sehingga diperoleh kuartil kedua = 160.
Untuk mencari kuartil pertama, mencari nilai median dari data yang lebih kecil dari kuartil kedua. Nilai di bawah kuartil kedua terdiri dari : 155, 155, 160, 160, dan 160. Jadi, median dari data di bawah kuartil kedua adalah (160 + 160) / 2 = 160.
Untuk mencari kuartil ketiga, mencari nilai median dari data yang lebih besar dari kuartil kedua. Nilai di atas kuartil kedua terdiri dari : 165, 165, 170, 170, dan 175. Jadi, median dari data di atas kuartil kedua adalah (170 + 170) / 2 = 170.
Sehingga diperoleh :
Kuartil Pertama (Q1) = 160
Kuartil Kedua (Q2) = 160
Kuartil Ketiga (Q3) = 170
Contoh Soal 2
Berikut adalah data interval tinggi badan siswa SMP dalam satuan cm :
| Kelas | Frekuensi |
|---|---|
| 150 – 155 | 2 |
| 155 – 160 | 3 |
| 160 – 165 | 3 |
| 165 – 170 | 4 |
| 170 – 175 | 3 |
Hitunglah kuartil pertama, kuartil kedua, dan kuartil ketiga.
Pembahasan
Langkah pertama adalah menentukan median atau kuartil kedua. N = ∑f = 15, sehingga nilai median atau kuartil kedua (Q2) adalah nilai ke-8 dari data yang telah diurutkan. Oleh karena itu, kita perlu mengetahui interval kelas untuk nilai ke-8. Dari tabel di atas, terdapat frekuensi kumulatif yang menyebar di interval kelas pada tabel tersebut :
| Kelas | Frekuensi | Frekuensi Kumulatif |
|---|---|---|
| 150 – 155 | 2 | 2 |
| 155 – 160 | 3 | 5 |
| 160 – 165 | 3 | 8 |
| 165 – 170 | 4 | 12 |
| 170 – 175 | 3 | 15 |
Dalam interval kelas 165 – 170, terdapat 12 data. Susunan data untuk interval ini adalah :
165, 165, 165, 165, 170, 170, 170, 170, 170, 170, 175, 175
Sehingga nilai median dari interval ini :
Q2 = 165 + (8 – 4) / 4 x 5
Q2 = 167.5
Setelah median atau kuartil kedua diketahui, selanjutnya kuartil pertama dan kuartil ketiga dapat dihitung dengan rumus :
Q1 = 160 + (15/4 – 5) / 3 x 5
Q1 = 156.67
Q3 = 167.5 + (15/4 – 8) / 4 x 5
Q3 = 170.83
Sehingga diperoleh :
Kuartil Pertama (Q1) = 156.67
Kuartil Kedua (Q2) = 167.5
Kuartil Ketiga (Q3) = 170.83
FAQ Kuartil
1. Apa Fungsi Kuartil dalam Menganalisis Data?
Kuartil sangat berguna dalam menganalisis data karena dapat digunakan untuk mengukur seberapa besar sebaran data. Selain itu, kuartil juga dapat membantu dalam menentukan letak data yang sering muncul (modus), mengetahui kisaran nilai data dan mengetahui letak nilai tengah dari data tersebut.
2. Apa Perbedaan antara Kuartil dan Persentil?
Kuartil merupakan nilai yang membagi data menjadi empat bagian yang sama besarnya, sedangkan persentil merupakan nilai yang membagi data menjadi seratus bagian yang sama besarnya. Artinya, persentil lebih rinci dalam menentukan posisi nilai dari suatu data yang dianalisis.
Video Youtube Kuartil
Berikut adalah video yang dapat menjadi sumber belajar tambahan mengenai kuartil :