Bilangan Biner Cara Menginstal Windows

Bilangan biner seringkali digunakan dalam dunia teknologi terutama di bidang komputer. Penggunaan bilangan biner dalam komputer sangatlah penting karena komputer hanya dapat memproses bilangan biner. Oleh karena itu, pemahaman tentang bilangan biner sangatlah penting bagi setiap orang yang ingin terjun ke dunia teknologi.

Bilangan Biner: Pengertian dan Contoh

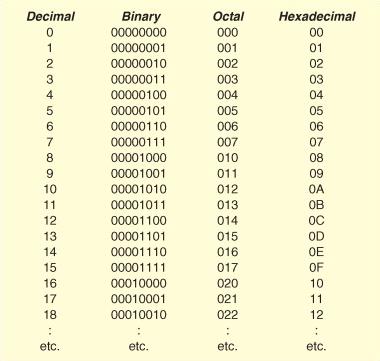
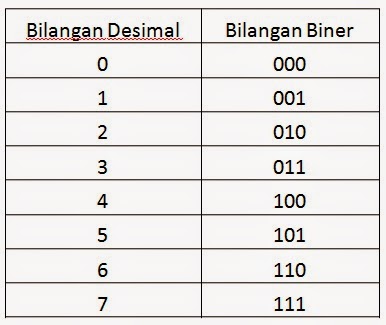
Bilangan biner adalah sistem bilangan yang hanya terdiri dari dua angka, yaitu 0 dan 1. Bilangan biner digunakan untuk merepresentasikan data dalam bentuk biner yang pada akhirnya akan diproses oleh komputer. Pada sistem bilangan biner, setiap angka memiliki nilai yang sama dengan yang terdapat pada sistem bilangan desimal pada posisi yang berlawanan dari kiri ke kanan. Salah satu contoh bilangan biner adalah 1001011 di mana 1 menggambarkan angka yang bernilai satu dan 0 menggambarkan angka yang bernilai nol.

Contoh di atas adalah bilangan biner dengan jumlah bit sebanyak 7. Dalam bilangan biner, seringkali kita menggunakan bit untuk merepresentasikan suatu angka. Setiap bit yang bernilai 1 akan melambangkan suatu nilai tertentu, sedangkan bit yang bernilai nol akan melambangkan nilai nol.

Cara Menghitung Bilangan Biner ke Oktal, Desimal, dan Hexadesimal

Salah satu cara untuk menghitung bilangan biner adalah dengan mengubahnya menjadi bilangan lain seperti bilangan oktal, desimal, atau hexadesimal. Berikut adalah cara untuk menghitung bilangan biner ke bilangan oktal, desimal, dan hexadesimal:

Menghitung Bilangan Biner ke Oktal

Langkah-langkah untuk menghitung bilangan biner ke oktal adalah sebagai berikut:

1. Bagi bit-bit bilangan biner menjadi kelompok tiga, dimulai dari bit paling kanan.
2. Tuliskan angka oktal yang sesuai dari setiap kelompok tiga bit tersebut.
3. Jika bit terakhir tidak membentuk kelompok tiga bit, tambahkan angka oktal yang sesuai untuk sisa bit tersebut.

Contoh:

Pada contoh di atas, bilangan biner 110110101001011 dibagi menjadi kelompok tiga bit (110) (110) (101) (001) (011). Selanjutnya, kita mengubah setiap kelompok tiga bit tersebut menjadi angka oktal yang sesuai. Dalam contoh ini, kita mendapatkan angka oktal 66513.

Menghitung Bilangan Biner ke Desimal

Langkah-langkah untuk menghitung bilangan biner ke desimal adalah sebagai berikut:

1. Tuliskan setiap bit dari bilangan biner ke dalam tabel.
2. Tuliskan pangkat 2 dengan eksponen yang dimulai dari 0 pada tabel di sebelah setiap bit, dimulai dari bit paling kanan.
3. Kalikan setiap bit dengan pangkat 2 yang sesuai.
4. Jumlahkan hasil kali dari langkah 3.

Contoh:

Kita akan menghitung bilangan biner 110110101001011 ke desimal. Pertama-tama, kita menuliskan bilangan biner tersebut ke dalam tabel:

1	1	0	1	1	0	1	0	1	0	0	1	0	1	1
20	21	22	23	24	25	26	27	28	29	210	211	212	213	214
1	1	0	1	1	0	1	0	1	0	0	1	0	1	1
	2		8	16		64		256			2048		8192	16384
	1		1	16		64		256			2048		8192	16384

Selanjutnya, kita mengalikan setiap bit dengan pangkat 2 yang sesuai untuk mendapatkan hasil kali seperti di bawah ini:

1	1	0	1	1	0	1	0	1	0	0	1	0	1	1
	2		8	16		64		256			2048		8192	16384
	2		8	16		64		256			2048		8192	16384
1	2	0	8	16	0	64	0	256	0	0	2048	0	8192	16384

Selanjutnya, kita menjumlahkan semua hasil kali di atas untuk mendapatkan hasil akhir, yaitu 6795.

Menghitung Bilangan Biner ke Hexadesimal

Langkah-langkah untuk menghitung bilangan biner ke hexadesimal adalah sebagai berikut:

1. Bagi bit-bit bilangan biner menjadi kelompok empat, dimulai dari bit paling kanan.
2. Tuliskan angka hexadesimal yang sesuai dari setiap kelompok empat bit tersebut.
3. Jika bit terakhir tidak membentuk kelompok empat bit, tambahkan angka hexadesimal yang sesuai untuk sisa bit tersebut.

Contoh:

Kita akan menghitung bilangan biner 110110101001011 ke hexadesimal. Pertama-tama, kita membagi bilangan biner tersebut menjadi kelompok empat bit seperti pada contoh di bawah ini:

Dalam contoh di atas, bilangan biner 1101 dibaca sebagai D, bilangan biner 1010 dibaca sebagai A, dan bilangan biner 1001 dibaca sebagai 9. Oleh karena itu, bilangan biner 110110101001011 dapat diubah menjadi nilai hexadesimal DA9.

FAQ

1. Apakah bilangan biner hanya terdiri dari angka 0 dan 1?

Ya, bilangan biner hanya terdiri dari angka 0 dan 1.

2. Apa saja contoh penggunaan bilangan biner dalam teknologi?

Bilangan biner banyak digunakan dalam teknologi, antara lain:

• Representasi data digital pada komputer
• Pengiriman data melalui jaringan komputer
• Enkripsi dan dekripsi data untuk keamanan informasi
• Pengendalian dan pengukuran dalam sistem otomasi

Video Pengenalan Bilangan Biner