Bagaimana Cara Menghitung Standar Deviasi Dengan Microsoft Excel

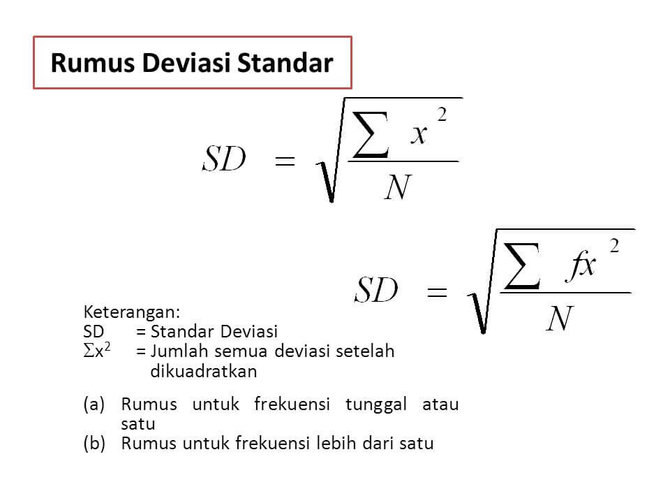
Standar deviasi adalah salah satu ukuran penting dalam statistik yang mengukur seberapa jauh data mengalami perbedaan atau deviasi dari rata-ratanya. Dalam pengolahan data, bisa jadi kita akan mencari standar deviasi dari sekumpulan data.

Menghitung Standar Deviasi di Excel

Salah satu cara untuk menghitung standar deviasi adalah dengan menggunakan Excel. Berikut adalah langkah-langkahnya:

1. Buatlah tabel data di Excel
2. Pilih sel tempat kita ingin menampilkan hasil perhitungan standar deviasi
3. Ketikkan formula =STDEV.s(range) pada sel tersebut
4. Tekan Enter pada keyboard

Range pada formula di atas adalah rentang sel data yang ingin kita hitung standar deviasinya. Contoh: =STDEV.s(A2:A10) artinya kita ingin menghitung standar deviasi dari sel A2 sampai A10.

Contoh Perhitungan Standar Deviasi di Excel

Pada tabel di atas, kita memiliki data nilai ujian siswa.

Lakukan langkah-langkah berikut untuk menghitung standar deviasi:

1. Pilih sel tempat kita ingin menampilkan hasil perhitungan standar deviasi (misalnya sel H2)
2. Ketikkan formula =STDEV.s(B2:B11) pada sel tersebut
3. Tekan Enter pada keyboard

Hasil perhitungan standar deviasi adalah 2,74.

Cara Mudah Menghitung Standar Deviasi di Excel 2010/2007

Berikut adalah contoh cara mudah menghitung standar deviasi di Excel 2010/2007 dengan fitur yang disediakan oleh Microsoft Excel:

1. Buka lembar kerja Excel yang berisi data yang akan dihitung standar deviasinya.
2. Pastikan bahwa area data yang akan dihitung telah dipilih dengan benar.
3. Pilih tab Formula, lalu pilih ikon More functions (fx) pada grup Function Library.
4. Pilih Statistical pada bagian Categories dan pilih STDEV.S pada bagian Functions.
5. Klik OK.
6. Gunakan kotak Range dalam kotak dialog Function Arguments untuk mengidentifikasi daftar nilai yang ingin dihitung.
7. Klik OK untuk menampilkan hasil pada sel yang dipilih sebelumnya.

Sekarang Anda sudah bisa menghitung standar deviasi di Excel dengan mudah menggunakan fitur yang disediakan oleh Microsoft Excel.

Cara Mencari Standar Deviasi Data Kelompok

Apabila kita memiliki data kelompok, kita bisa menghitung standar deviasinya dengan menggunakan formula yang berbeda. Berikut adalah langkah-langkahnya:

1. Buatlah tabel data kelompok
2. Hitunglah rata-rata dari masing-masing grup data
3. Tentukan nilai tengah dari masing-masing grup data
4. Tentukan frekuensi masing-masing grup data
5. Hitunglah standar deviasi menggunakan rumus berikut:
   
   Standar deviasi = akar dari (jumlah tiap frekuensi dikali dengan kuadrat selisih antara nilai tengah dan rata-rata, semua di bagi dengan jumlah total data minus 1)

Berikut adalah contoh perhitungan standar deviasi data kelompok:

Pada tabel di atas, kita memiliki data kelompok yang terdiri dari beberapa rentang nilai.

Lakukan langkah-langkah berikut untuk menghitung standar deviasi:

1. Hitunglah rata-rata dari masing-masing grup data
   
   Rata-rata grup 1 = 75 + 78 + 88 + 90 / 4 = 82,75
   
   Rata-rata grup 2 = 71 + 72 + 83 + 87 + 100 / 5 = 82,6
   
   Rata-rata grup 3 = 72 + 74 + 80 + 81 / 4 = 76,75
   
   Rata-rata grup 4 = 77 + 82 + 85 / 3 = 81,33
2. Tentukan nilai tengah dari masing-masing grup data
   
   Nilai tengah grup 1 = 82,5
   
   Nilai tengah grup 2 = 82,5
   
   Nilai tengah grup 3 = 77
   
   Nilai tengah grup 4 = 82
3. Tentukan frekuensi masing-masing grup data
   
   Frekuensi grup 1 = 4
   
   Frekuensi grup 2 = 5
   
   Frekuensi grup 3 = 4
   
   Frekuensi grup 4 = 3
4. Hitunglah standar deviasi menggunakan rumus berikut:
   
   Standar deviasi = akar dari (((4 x (82,5 – 82,75) ²) + (4 x (88 – 82,75) ²) + (4 x (90 – 82,75) ²) + (4 x (75 – 82,75) ²)) + ((5 x (71 – 82,6) ²) + (5 x (72 – 82,6) ²) + (5 x (83 – 82,6) ²) + (5 x (87 – 82,6) ²) + (5 x (100 – 82,6) ²)) + ((4 x (72 – 77) ²) + (4 x (74 – 77) ²) + (4 x (80 – 77) ²) + (4 x (81 – 77) ²)) + ((3 x (77 – 81,33) ²) + (3 x (82 – 81,33) ²) + (3 x (85 – 81,33) ²))) / (20 – 1))
   
   Standar deviasi = 5,31

Jadi standar deviasi dari data kelompok di atas adalah sebesar 5,31.

FAQ

Apa manfaat dari menghitung standar deviasi?

Menghitung standar deviasi berguna untuk mengukur seberapa jauh data terdistribusi dari rata-ratanya. Dengan memahami standar deviasi, kita dapat mengevaluasi bagaimana variabilitas data dalam kelompok dan memprediksi perilaku data di masa mendatang.

Bagaimana cara menginterpretasikan hasil standar deviasi?

Hasil standar deviasi yang kecil menunjukkan bahwa data cenderung berkumpul di sekitar rata-ratanya atau kurang variatif, sedangkan hasil standar deviasi yang besar menunjukkan bahwa data cenderung berbeda jauh dari rata-ratanya atau sangat variatif. Perlu diingat bahwa hasil standar deviasi harus dilihat dalam konteks data yang sedang dipelajari.

Video Tutorial

Berikut adalah video tutorial mengenai cara menghitung standar deviasi di Excel:

Semoga artikel ini bermanfaat bagi Anda yang sedang belajar mengenai standar deviasi dan cara menghitungnya di Excel. Terima kasih sudah membaca!