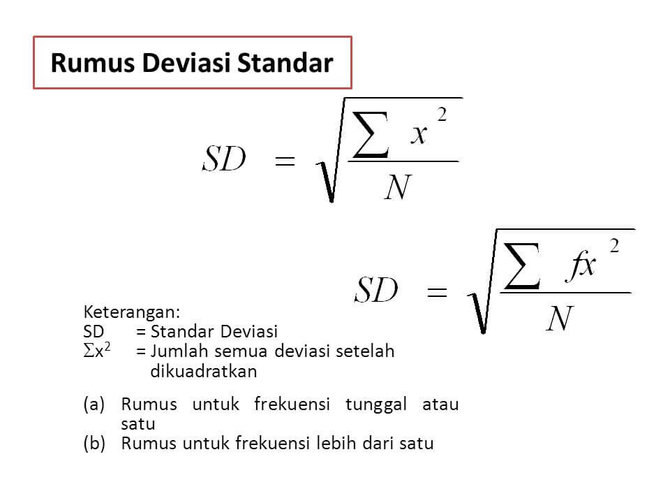
Standar Deviasi dan Varians adalah alat pengukuran statistik yang digunakan untuk menghitung seberapa jauh data tersebar dari nilai rata-ratanya. Dalam artikel ini, kita akan membahas cara menghitung Standar Deviasi dan Varians untuk data berkelompok serta memberikan penjelasan lebih lanjut mengenai kedua konsep ini.
Cara Menghitung Varians Data Berkelompok Contoh soal Varians Data
Sebelum kita masuk ke rumus perhitungan Varians data berkelompok, mari kita perhatikan contoh soal di bawah ini. Diketahui data berikut ini:
- A
- B
- C
- D
- E
| Kelas | Frekuensi | Nilai Tengah (xi) | xi^2 | fxi |
|---|---|---|---|---|
| 0 – 10 | 5 | 5 | 25 | 25 |
| 10 – 20 | 10 | 15 | 225 | 150 |
| 20 – 30 | 12 | 25 | 625 | 300 |
| 30 – 40 | 8 | 35 | 1225 | 280 |
| 40 – 50 | 5 | 45 | 2025 | 225 |
Dalam contoh soal di atas, data telah dikelompokkan berdasarkan kisaran nilai yang dimiliki oleh setiap data. Kita dapat menggunakan rumus berikut untuk menghitung Varians data berkelompok:
Dalam rumus ini, N merupakan jumlah data dalam setiap kelas, n merupakan jumlah kelas, Xi merupakan nilai tengah dari setiap kelas, dan fi merupakan frekuensi dari setiap kelas. Berdasarkan data pada contoh soal di atas, kita dapat menghitung nilai rata-rata (X), varian, dan standar deviasi sebagai berikut:
Rata-rata (X) = 558/40 = 13.95
Varian = [(25(5)+225(10)+625(12)+1225(8)+2025(5))/40] – (13.95)^2 = 271.97
Standar Deviasi = akar dari Varian = akar(271.97) = 16.48
Rumus Validasi Data Excel
Rumus perhitungan Varians dan Standar Deviasi juga tersedia di Microsoft Excel dengan menggunakan fungsi AVERAGE, VAR, dan STDEV.S. Untuk menghitung Varians atau Standar Deviasi dalam Excel, kita dapat mengikuti langkah-langkah berikut:
- Pilih sel tempat kita ingin menampilkan hasil.
- Ketikkan formula =VAR.S(data) atau =STDEV.S(data) untuk menghitung Varians atau Standar Deviasi pada data yang tidak berkelompok.
- Untuk menghitung Varians atau Standar Deviasi pada data berkelompok, kita dapat menggunakan rumus =VAR.P(data) atau =STDEV.P(data) di mana data adalah rentang sel yang mengandung data kita. Pilih sel tempat kita ingin menampilkan hasil, ketikkan rumus yang sesuai, dan tekan enter untuk melihat hasilnya.
Cara Mencari Standar Deviasi Data Kelompok – iFaWorldCup.com
Untuk menghitung Standar Deviasi data kelompok, kita dapat mengikuti langkah-langkah berikut:
- Menghitung nilai tengah (xi) dari setiap kelas.
- Menghitung frekuensi relatif (fri) dari setiap kelas dengan rumus fri = fi/N di mana fi adalah frekuensi dari setiap kelas dan N adalah total frekuensi dari seluruh kelas.
- Menghitung total frekuensi (N).
- Hitung nilai tengah rata-rata (X) dengan menggunakan rumus X = sigma[fri*xi].
- Hitung varians dengan rumus sigma[fri*(xi-X)^2].
- Menghitung Standar Deviasi dengan menghitung akar kuadrat dari Varians.
Rumus Excel Standar Deviasi – My Blog
Bagi pengguna Excel yang ingin menghitung Standar Deviasi dari data, Anda dapat menggunakan fungsi STDEV.P atau STDEV.S. Rumus lengkapnya seperti di bawah ini:
STDEV.P(data) = Standar Deviasi Populasi data
STDEV.S(data) = Standar Deviasi Sampel data
Dalam kedua formula tersebut, data adalah range sel Excel yang berisi data yang akan dihitung Standar Deviasinya. Untuk memahami perbedaan antara Standar Deviasi Populasi dan Standar Deviasi Sampel, mari kita lihat penjelasan di bawah ini:
- Standar Deviasi Populasi digunakan untuk menghitung Standar Deviasi dari seluruh populasi data.
- Standar Deviasi Sampel digunakan untuk menghitung Standar Deviasi dari sampel data yang diambil dari populasi secara acak.
FAQs
1. Mengapa Standar Deviasi penting dalam analisis data?
Standar Deviasi penting dalam analisis data karena dapat memberikan informasi mengenai seberapa jauh data tersebar dari nilai rata-rata. Hal ini dapat membantu kita untuk mengetahui apakah suatu data relatif homogen atau heterogen. Semakin tinggi Standar Deviasi, semakin besar kemungkinan data tersebar secara luas di sekitar nilai rata-rata. Dalam beberapa kasus, Standar Deviasi juga dapat memberikan informasi mengenai sebaran data normal dalam distribusi normal.
2. Apa perbedaan antara Standar Deviasi Populasi dan Standar Deviasi Sampel?
Standar Deviasi Populasi dan Standar Deviasi Sampel merupakan dua metode untuk menghitung Standar Deviasi. Perbedaannya terletak pada data yang dipakai. Standar Deviasi Populasi digunakan untuk menghitung Standar Deviasi dari seluruh populasi data, sedangkan Standar Deviasi Sampel digunakan untuk menghitung Standar Deviasi dari sampel data yang diambil dari populasi secara acak. Dalam praktek, Standar Deviasi Populasi sering digunakan ketika kita memiliki data lengkap dari suatu populasi, sementara Standar Deviasi Sampel sering digunakan ketika kita hanya memiliki data sampel dari suatu populasi.
Video Tutorial: Cara Menghitung Standar Deviasi