Data statistik seringkali menjadi pusat perhatian dalam analisis sebuah fenomena. Hal ini karena data dapat membantu kita untuk mengidentifikasi pola, tren, dan variabel yang mungkin berpengaruh terhadap hasil yang diinginkan. Dalam analisis statistik, salah satu metode yang seringkali digunakan adalah standar deviasi. Di sini kita akan membahas cara mencari standar deviasi pada data kelompok.
Cara Mencari Standar Deviasi Data Kelompok
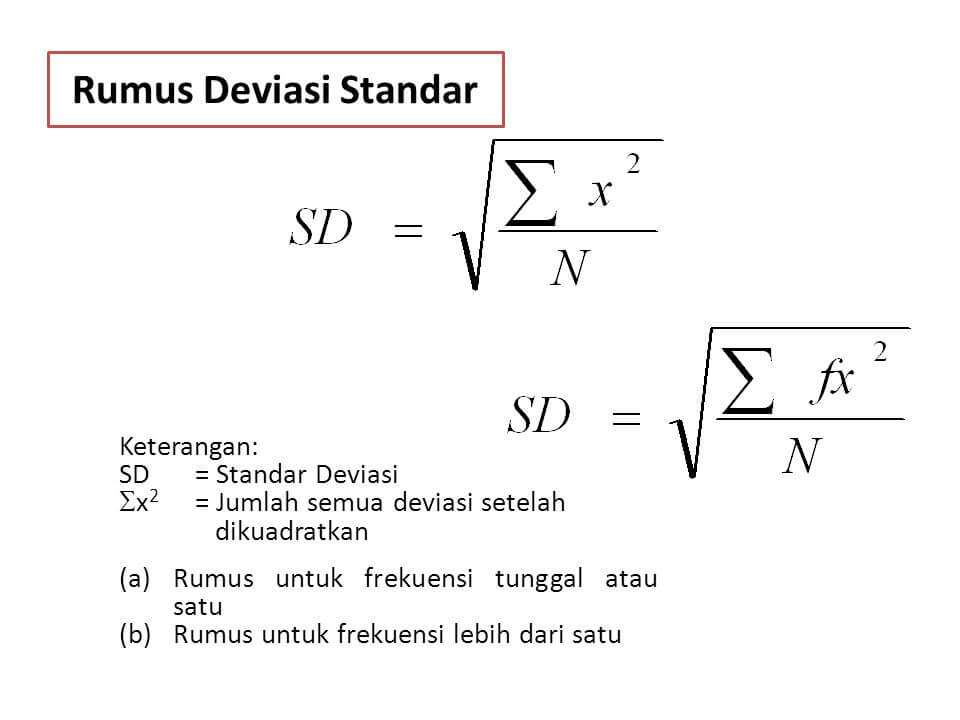
Sebelum membahas lebih lanjut, kita harus memahami terlebih dahulu apa itu standar deviasi. Standar deviasi adalah ukuran statistik yang dikenal juga sebagai simpangan baku yang digunakan untuk mengukur seberapa tersebar atau variatif data dari rata-ratanya.
Namun, dalam prakteknya mencari standar deviasi pada data kelompok tidak semudah seperti mencari standar deviasi pada data tunggal. Ada beberapa tahap yang harus dilakukan, diantaranya:
Mulai dengan menghitung rata-rata
Langkah pertama dalam mencari standar deviasi data kelompok adalah dengan menghitung rata-rata dari setiap kelompok data. Rumusnya sebagai berikut:
Contoh: Misalkan kita memiliki data kelompok seperti berikut:
| Kelompok | Data | Rata-rata |
|---|---|---|
| A | 1 | |
| 2 | ||
| 3 | ||
| 4 | ||
| 5 |
Kita dapat menghitung rata-rata dari kelompok A dengan menggunakan rumus berikut:
Jadi, rata-rata dari kelompok A adalah 3.
Hitung selisih kuadrat
Setelah kita menghitung rata-rata dari setiap kelompok data, langkah selanjutnya adalah menghitung selisih kuadrat. Selisih kuadrat adalah nilai yang diperoleh dari pengurangan setiap data dengan rata-rata dan kemudian hasilnya dipangkatkan dua. Rumusnya sebagai berikut:
Contoh: Kembali pada data kelompok A, misalkan kita telah menghitung rata-rata yang telah disebutkan sebelumnya. Selanjutnya kita harus menghitung selisih kuadrat untuk masing-masing data. Rumusnya sebagai berikut:
Jadi, selisih kuadrat dari data 1 pada kelompok A adalah:
Selisih kuadrat dari data lain dapat dihitung dengan cara yang sama. Kemudian kita bisa menghitung jumlah selisih kuadrat pada setiap kelompok data.
Menghitung standar deviasi
Setelah kita menghitung selisih kuadrat dari setiap data dan jumlahnya, kita dapat menghitung standar deviasi dengan rumus berikut:
Contoh: Mari kita hitung standar deviasi untuk kelompok A pada data kita. Berikut jumlah selisih kuadrat dan rumus untuk menghitung standar deviasi:
Berarti, standar deviasi pada kelompok A adalah 1.41.
FAQ (Frequently Asked Questions)
Ya, standar deviasi yang lebih rendah menunjukkan data yang lebih homogen atau lebih terkonsentrasi di sekitar rata-rata. Sedangkan standar deviasi yang lebih tinggi menunjukkan data yang lebih heterogen atau lebih tersebar dari rata-rata.
2. Berapa banyak data minimum yang dibutuhkan untuk menggunakan rumus standar deviasi?
Untuk menggunakan rumus standar deviasi dengan baik, biasanya dibutuhkan minimal 30 sampel data. Namun, jika sampel data yang tersedia lebih sedikit, masih bisa menggunakan rumus standar deviasi, tetapi dengan hati-hati dalam interpretasi hasilnya.
Demikian penjelasan mengenai cara mencari standar deviasi data kelompok dan jawaban atas pertanyaan yang sering ditanyakan. Semoga bermanfaat untuk Anda yang sedang belajar tentang analisis statistik. Terima kasih sudah membaca.