Matematika mungkin bisa dibilang sebagai subjek yang paling menantang bagi beberapa orang. Namun, ada beberapa konsep matematika yang sangat penting dan bahkan digunakan dalam kehidupan sehari-hari. Salah satunya adalah matriks. Matriks adalah kumpulan bilangan yang disusun dalam sebuah tabel. Pada artikel ini, kita akan membahas beberapa konsep matriks termasuk cara menghitung, mengubah, dan bahkan menginversi matriks.
Cara Menghitung Nilai Tertinggi (Fungsi MAX) Secara Otomatis Pada Matriks
Saat bekerja dengan matriks, sering kali kita perlu mencari nilai tertinggi dalam sebuah baris atau kolom. Jika kita menggunakan tabel berukuran kecil, maka kita bisa dengan mudah mencari nilai tertinggi secara manual. Namun, pada tabel yang lebih besar, mencari nilai tertinggi secara manual bisa menjadi tugas yang sangat membosankan dan memakan waktu. Oleh karena itu, ada fungsi di Excel yang bisa membantu kita mencari nilai tertinggi secara otomatis, yaitu fungsi MAX.
Sebelum kita menghitung nilai tertinggi, kita harus terlebih dahulu memahami cara membaca dan menentukan letak baris dan kolom dalam matriks. Secara umum, kita bisa memasukkan data ke dalam matriks dengan cara berikut:
Contohnya, jika kita ingin mencari nilai tertinggi dari colom A pada contoh matriks di atas, maka kita bisa menggunakan fungsi MAX seperti ini:
=MAX(A1:A3)
Dalam hal ini, fungsi MAX akan mencari nilai tertinggi dari sel A1 hingga A3 dalam matriks. Maka, hasilnya akan menjadi 10. Kita juga bisa menggunakan fungsi MAX untuk mencari nilai tertinggi dalam sebuah baris matriks seperti ini:
=MAX(A1:C1)
Dalam hal ini, fungsi MAX akan mencari nilai tertinggi dari sel A1 hingga C1 dalam matriks. Maka, hasilnya akan menjadi 7.
Determinan Matriks 3×3
Determinan matriks 3×3 adalah salah satu konsep matriks yang paling penting. Determinan adalah angka yang terkait dengan matriks dan memiliki sifat matematis tertentu. Ada beberapa cara untuk menghitung determinan matriks, dan salah satunya adalah dengan menggunakan aturan Sarrus. Aturan Sarrus adalah cara yang mudah dan cepat untuk menghitung determinan matriks 3×3.
Sebelum memahami bagaimana menggunakan aturan Sarrus, pertama-tama kita harus tahu bagaimana cara menyusun matriks 3×3. Secara umum, matriks 3×3 adalah matriks yang terdiri dari 3 baris dan 3 kolom. Misalnya, consider this matrix:
Untuk menghitung determinan matriks 3×3 menggunakan aturan Sarrus, Anda perlu membuat dua baris tambahan di bawah baris matriks. Selanjutnya, Anda dapat menuliskan angka-angka matriks, seperti dalam contoh ini:
Setelah itu, Anda dapat menghitung determinan matriks 3×3 dengan menggunakan aturan Sarrus:
det(A) = (a x e x i) + (b x f x g) + (c x d x h) - (c x e x g) - (a x f x h) - (b x d x i)
Misalkan kita memiliki matriks berikut:
A = [3 4 2; 5 1 3; 2 4 6]
Untuk menghitung determinan matriks ini, Anda dapat memasukkan nilai dari matriks ke rumus aturan Sarrus, seperti ini:
det(A) = (3 x 1 x 6) + (4 x 3 x 2) + (2 x 5 x 4) - (2 x 1 x 2) - (3 x 4 x 6) - (4 x 5 x 3)
Hasilnya adalah det(A)= -54. Dalam aplikasi di dunia nyata, determinan matriks 3×3 dapat digunakan dalam berbagai aplikasi, termasuk perhitungan geografi dan fisika.
Cara Mengubah Matriks ke Bentuk Baris Tereduksi
Sekarang Anda sudah tahu bagaimana cara menghitung nilai tertinggi dan determinan matriks 3×3. Namun, ada juga teknik matriks yang berguna, terutama ketika berurusan dengan matriks besar. Teknik ini disebut bentuk baris tereduksi atau dalam bahasa Inggris disebut row echelon form.
Baris tereduksi adalah bentuk matriks di mana setiap baris yang mengandung elemen nol di atas elemen bukan nol terletak di bawah setiap baris yang mengandung elemen bukan nol. Baris tereduksi sangat berguna dalam berbagai aplikasi teknik dan statistik. Untuk mengubah matriks ke dalam bentuk baris tereduksi, Anda dapat menggunakan beberapa metode, seperti metode Gauss atau metode Gauss-Jordan.
Seperti determinan matriks, teknik row echelon juga bisa diaplikasikan ke matriks 3×3. Dalam contoh ini, kita akan membahas bagaimana cara mengubah matriks 3×3 menjadi bentuk baris tereduksi. Pertama, pastikan bahwa matriks Anda sudah digunakan dengan aturan Sarrus. Kemudian, Anda bisa menggunakan baris pertama sebagai titik awal. Caranya adalah dengan mencari elemen bukan nol pertama dan membagi seluruh baris dengan elemen tersebut.
Misalkan kita memiliki matriks berikut:
A = [1 2 3; 4 5 6; 7 8 9]
Pertama, kita mencari elemen bukan nol pada baris pertama, yaitu 1. Kemudian, kita membagi seluruh baris 1 dengan 1:
1 2 3 | 1 2 3 0 3 6 | 3 3 3 0 0 0 | 0 0 0
Setelah itu, kita bisa menggunakan baris kedua sebagai titik awal untuk mencari elemen bukan nol kedua dan membagi seluruh baris dengan elemen tersebut:
1 2 3 | 1 2 3 0 1 2 | 1 1 1 0 0 0 | 0 0 0
Terkahir, kita menggunakan baris ketiga sebagai titik awal untuk mencari elemen bukan nol ketiga dan membagi seluruh baris dengan elemen tersebut:
1 2 3 | 1 2 3 0 1 2 | 1 1 1 0 0 0 | 0 0 0
Setelah semua baris sudah diberi nomor dan semua elemen nol berada di bawah elemen bukan nol, maka kita sudah mendapatkan bentuk baris tereduksi dari matriks awal.
Cara Mencari Invers Matriks Ordo 2×2 dan 3×3
Membalikkan sebuah matriks adalah salah satu konsep matriks yang paling penting dan berguna. Ketika kita membalikkan sebuah matriks, kita diberikan matriks yang memiliki sifat unik dan berguna dalam berbagai aplikasi di matematika dan teknik. Untuk membalikkan sebuah matriks, kita memerlukan metode tersendiri yang biasanya disebut dengan mencari invers matriks.
Untuk mencari invers matriks, Anda harus merujuk pada dua konsep yang sebelumnya dibahas, yaitu determinan matriks dan bentuk baris tereduksi. Anda juga harus memahami konsep baru, yaitu matriks kofaktor dan Adjoint. Matriks kofaktor adalah matriks yang terbentuk dari determinan matriks yang telah dihilangkan baris dan kolom tertentu. Adjoint adalah matriks kofaktor yang dicerminkan dalam diagonal utama.
Untuk mencari invers matriks ordo 2×2, Anda bisa menggunakan rumus sederhana berikut:
A^-1 = 1 / det(A) * [d -b; -c a]
Dimana A adalah matriks awal, A^-1 adalah matriks hasil invers, a, b, c, dan d adalah elemen-elemen dari matriks A, dan det(A) adalah determinan matriks A. Mari kita hitung invers matriks untuk matriks 2×2 berikut:
A = [2 3; 5 7]
Nomor pertama adalah menghitung determinan matriks, seperti ini:
det(A) = (2 * 7) - (3 * 5) = -1
Kemudian kita memasukkan nilai-nilai ini ke dalam rumus invers matriks:
A^-1 = 1 / (-1) * [7 -3; -5 2]
Maka, hasilnya adalah:
A^-1 = [-7 3; 5 -2]
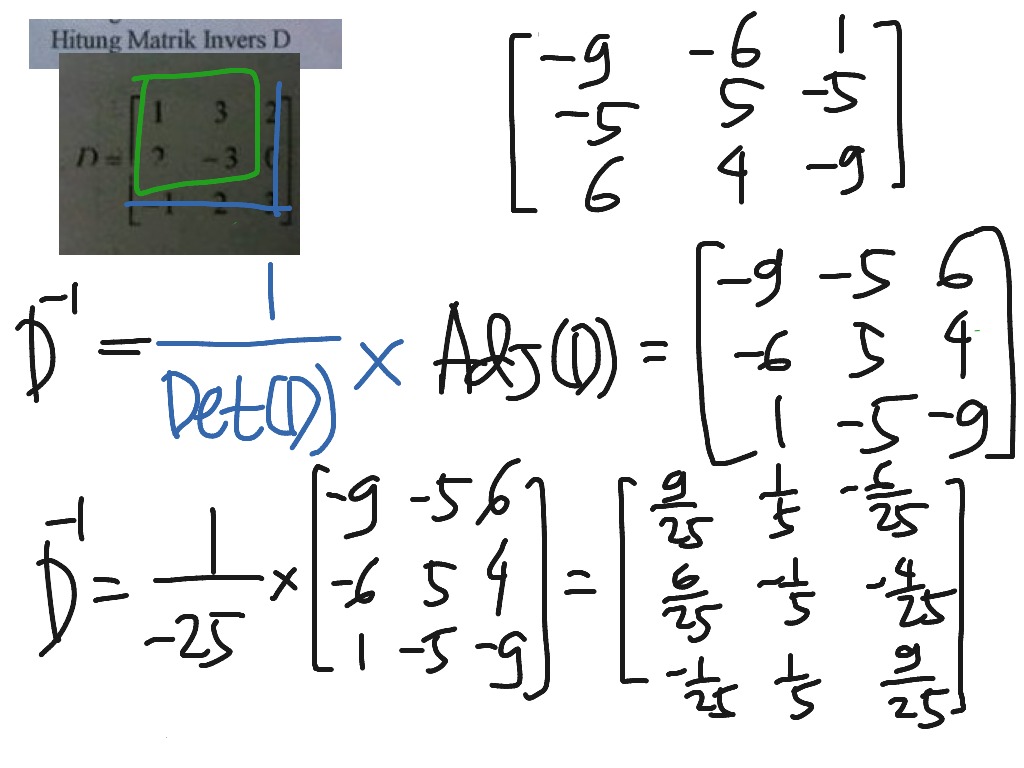
Untuk mencari invers matriks ordo 3×3, Anda bisa menggunakan rumus berikut:
A^-1 = 1 / det(A) * adj(A)
Yang mana A adalah matriks awal, A^-1 adalah matriks hasil invers, det(A) adalah determinan matriks A, dan adj(A) adalah Adjoint matriks A. Mari kita hitung invers matriks untuk matriks 3×3 berikut:
A = [1 2 3; 0 1 4; 5 6 0]
Nomor pertama adalah menghitung determinan matriks, seperti ini:
det(A) = (1 * 1 * 0) + (2 * 4 * 5) + (3 * 0 * 6) - (3 * 1 * 5) - (2 * 0 * 0) - (1 * 4 * 0) = -23
Selanjutnya, kita akan menghitung matriks kofaktor dan Adjoint. Matriks kofaktor dihitung dari determinan matriks yang telah dihilangkan baris dan kolom tertentu. Dalam contoh ini, matriks kofaktor kita dapatkan seperti ini:
C = [-24 -12 2; 18 -6 -3; 3 6 -2]
Lalu, kita mendapatkan Adjoint matriks A dengan memutar matriks kofaktor seperti ini:
adj(A) = [-24 18 3; -12 -6 6; 2 -3 -2]
Setelah mendapatkan nilai dari det(A) dan adj(A), kita bisa memasukkan nilai-nilai ini ke dalam rumus invers matriks:
A^-1 = 1 / (-23) * [-24 18 3; -12 -6 6; 2 -3 -2]
Hasilnya adalah:
A^-1 = [4/23 -6/23 3/23; -5/69 1/23 2/69; 2/23 2/23 -1/23]
FAQ
1. Apa itu matriks?
Matriks adalah kumpulan bilangan yang disusun dalam sebuah tabel. Matriks memiliki banyak aplikasi dalam berbagai bidang, terutama dalam teknik dan ilmu pengetahuan.
2. Apa yang dimaksud dengan determinan matriks?
Determinan matriks adalah sebuah angka yang terkait dengan matriks dan memiliki sifat matematis tertentu. Determinan matriks sangat berguna dalam berbagai aplikasi, termasuk perhitungan geografi dan fisika.
Video di Youtube
Berikut adalah video yang membahas tentang konsep matriks lebih detail: