Saat mempelajari matematika, kita pasti akan mengenal banyak sekali konsep dan rumus. Salah satu konsep penting yang harus dipelajari adalah matriks. Matriks adalah susunan angka dalam tabel persegi atau persegi panjang. Konsep matriks digunakan untuk merepresentasikan data dalam bentuk tabel yang kompleks, sehingga memudahkan untuk melakukan perhitungan matematika. Dalam artikel kali ini, kita akan membahas beberapa konsep yang terkait dengan matriks, seperti perkalian matriks, determinan matriks, dan cara membuat matriks.
Perkalian Matriks
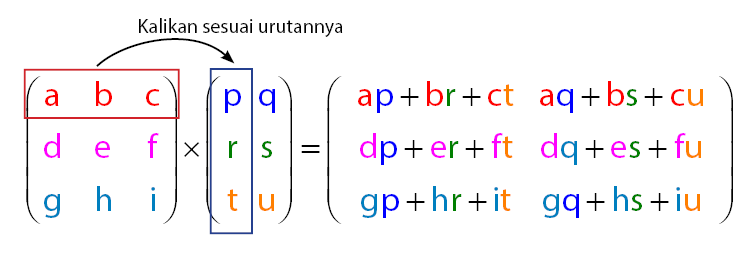
Perkalian matriks adalah salah satu operasi matriks yang paling penting. Perkalian matriks dapat dilakukan jika jumlah kolom matriks pertama sama dengan jumlah baris matriks kedua. Dalam contoh ini, kita akan mengalikan matriks A dan matriks B:
Hasil perkalian matriks A dan B adalah:

Perkalian matriks juga dapat dilakukan dengan menggunakan software seperti Microsoft Excel. Caranya adalah:
- Buka Microsoft Excel
- Ketikkan matriks pertama di dalam sebuah rentang sel, dan matriks kedua di dalam rentang sel yang berbeda. Pastikan jumlah kolom matriks pertama sama dengan jumlah baris matriks kedua.
- Pilih sel tempat Anda ingin menampilkan hasil perkalian matriks, dan ketikkan formula =MMULT(matrix1,matrix2), lalu tekan Enter.
Determinan Matriks
Determinan matriks merupakan nilai yang diperoleh dari operasi matematika tertentu terhadap suatu matriks. Nilai determinan matriks berfungsi untuk menentukan apakah suatu matriks invers dapat diperoleh atau tidak. Dalam contoh ini, kita akan menghitung determinan matriks 3×3:
Untuk menghitung determinan matriks 3×3, kita dapat menggunakan rumus berikut:

Hasil dari perhitungan determinan matriks pada contoh di atas adalah:

Cara Membuat Matriks
Untuk membuat matriks, kita dapat menggunakan Microsoft Excel. Caranya adalah:
- Buka Microsoft Excel
- Pilih tab “Insert”, dan klik “Table”.
- Pilih ukuran tabel yang diinginkan dan klik “Create”.
- Isi tabel dengan data yang diinginkan.
FAQ
1. Apa itu transpose matriks?
Transpose matriks adalah sebuah proses meningkatkan baris menjadi kolom dan kolom menjadi baris pada sebuah matriks. Jadi, hasil transpose dari matriks dengan ukuran mxn akan menghasilkan matriks dengan ukuran nxm.
2. Apa itu invers matriks?
Invers matriks adalah matriks yang jika dikalikan dengan matriks asalnya akan menghasilkan matriks identitas. Invers matriks hanya dapat ditemukan pada matriks-kolibri, yaitu matriks yang memiliki determinan tidak sama dengan nol.
Video Tutorial: Rumus Perkalian Matriks pada Microsoft Excel
Berikut adalah video tutorial yang dapat membantu Anda memahami cara melakukan perkalian matriks pada Microsoft Excel:
Dalam artikel ini, kita telah membahas beberapa konsep matriks, seperti perkalian matriks, determinan matriks, dan cara membuat matriks. Semoga artikel ini dapat membantu Anda memahami konsep matriks dengan lebih baik.