Segitiga adalah salah satu bentuk bangun datar yang paling sering ditemui dalam kehidupan sehari-hari. Selain memiliki sifat-sifat yang menarik, luas dan keliling segitiga juga sering dihitung dalam berbagai situasi, baik di lingkungan sekolah ataupun dalam kehidupan profesional. Oleh karena itu, pada artikel kali ini, kita akan membahas tentang cara menghitung luas dan keliling segitiga, bersama dengan contoh soal dan pembahasannya.
Cara Menghitung Luas Segitiga
Luas segitiga merupakan luas bidang yang dikelilingi oleh tiga sisi segitiga. Rumus untuk menghitung luas segitiga adalah:
L = 1/2 x alas x tinggi
Di mana L merupakan luas segitiga, alas merupakan panjang salah satu sisi segitiga, dan tinggi merupakan jarak titik tengah sisi yang dipilih dengan sisi yang tegak lurus terhadap sisi tersebut. Berikut ini adalah contoh penggunaan rumus tersebut untuk menghitung luas segitiga:
Contoh 1: Hitunglah luas segitiga dengan alas 8 cm dan tinggi 6 cm.
Penyelesaian:
L = 1/2 x 8 cm x 6 cm
L = 24 cm2
Jadi, luas segitiga dengan alas 8 cm dan tinggi 6 cm adalah 24 cm2.
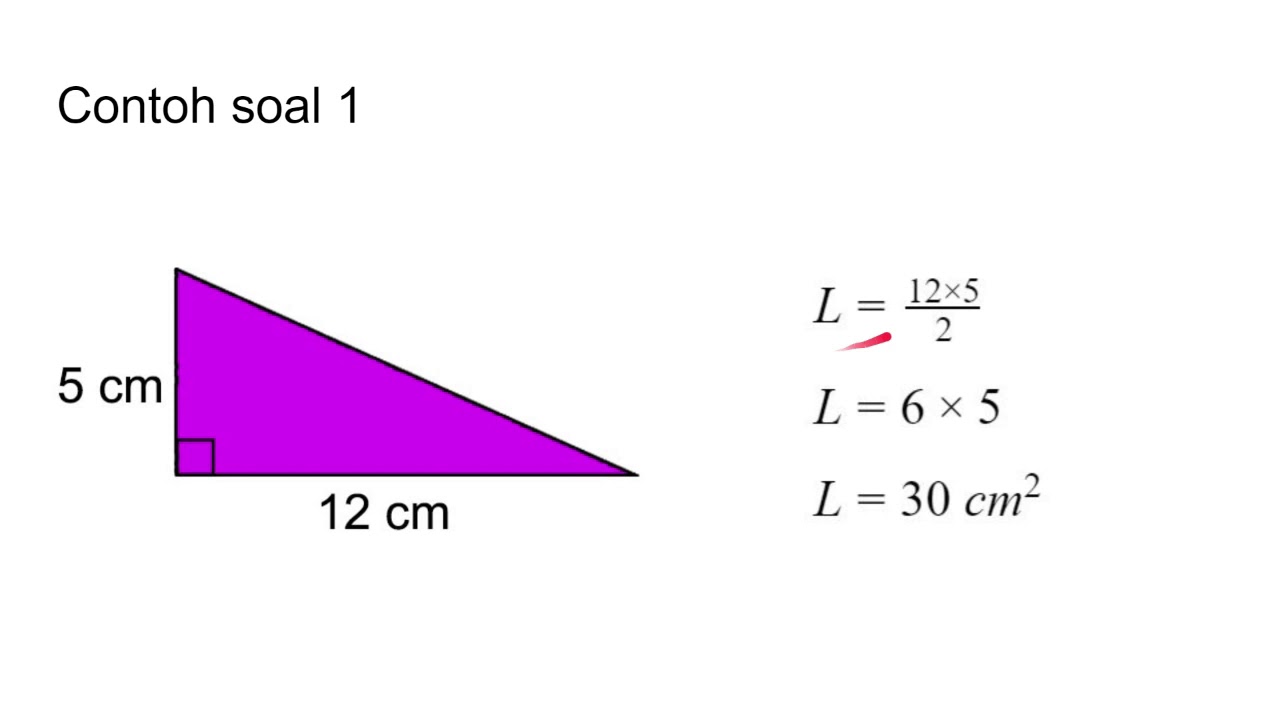
Contoh 2: Hitunglah luas segitiga dengan alas 12 cm dan tinggi 5 cm.
Penyelesaian:
L = 1/2 x 12 cm x 5 cm
L = 30 cm2
Sehingga, luas segitiga dengan alas 12 cm dan tinggi 5 cm adalah 30 cm2.
Berikut ini adalah beberapa contoh soal lainnya beserta pembahasannya:
Contoh 3: Hitunglah luas segitiga dengan alas 16 cm dan tinggi 8 cm.
Penyelesaian:
L = 1/2 x 16 cm x 8 cm
L = 64 cm2
Jadi, luas segitiga dengan alas 16 cm dan tinggi 8 cm adalah 64 cm2.
Contoh 4: Hitunglah luas segitiga dengan alas 10 cm dan tinggi 12 cm.
Penyelesaian:
L = 1/2 x 10 cm x 12 cm
L = 60 cm2
Sehingga, luas segitiga dengan alas 10 cm dan tinggi 12 cm adalah 60 cm2.
Bagaimana jika segitiga yang akan dihitung luasnya tidak memiliki tinggi? Pada kasus ini, dapat digunakan teorema Pythagoras untuk mencari tinggi segitiga. Teorema Pythagoras menyatakan bahwa pada segitiga siku-siku, kuadrat dari panjang sisi miring sama dengan jumlah kuadrat dari panjang sisi-sisi yang lain. Dengan demikian, dapat ditemukan tinggi segitiga tersebut, dan kemudian dapat digunakan untuk menghitung luasnya.
Contoh 5: Hitunglah luas segitiga dengan panjang sisi-sisi 5 cm, 12 cm, dan 13 cm.
Penyelesaian:
Pertama-tama, perlu dicari tahu apakah segitiga tersebut merupakan segitiga siku-siku atau tidak. Diketahui:
52 + 122 = 169
132 = 169
Karena 52 + 122 sama dengan 132, maka segitiga tersebut dapat dikategorikan sebagai segitiga siku-siku. Selanjutnya, dapat dicari tinggi segitiga menggunakan teorema Pythagoras:
132 = 52 + h2
169 = 25 + h2
h2 = 144
h = 12 cm
Dengan demikian, tinggi segitiga adalah 12 cm dan luas segitiga dapat dihitung seperti contoh sebelumnya:
L = 1/2 x 5 cm x 12 cm
L = 30 cm2
Jadi, luas segitiga dengan panjang sisi-sisi 5 cm, 12 cm, dan 13 cm adalah 30 cm2.
Cara Menghitung Keliling Segitiga
Keliling segitiga merupakan panjang total dari ketiga sisi segitiga. Rumus untuk menghitung keliling segitiga adalah:
K = a + b + c
Di mana K merupakan keliling segitiga, a, b, dan c masing-masing adalah panjang sisi segitiga. Berikut ini adalah contoh penggunaan rumus tersebut untuk menghitung keliling segitiga:
Contoh 1: Hitunglah keliling segitiga dengan panjang sisi 6 cm, 8 cm, dan 10 cm.
Penyelesaian:
K = 6 cm + 8 cm + 10 cm
K = 24 cm
Jadi, keliling segitiga dengan panjang sisi 6 cm, 8 cm, dan 10 cm adalah 24 cm.
Contoh 2: Hitunglah keliling segitiga dengan panjang sisi 12 cm, 15 cm, dan 20 cm.
Penyelesaian:
K = 12 cm + 15 cm + 20 cm
K = 47 cm
Sehingga, keliling segitiga dengan panjang sisi 12 cm, 15 cm, dan 20 cm adalah 47 cm.
Perlu diingat bahwa pada segitiga, salah satu sisi tidak dapat lebih panjang dari jumlah kedua sisi lainnya. Jika hal ini terjadi, maka segitiga tersebut tidak dapat dibentuk. Jadi, sebelum menghitung keliling segitiga, pastikan terlebih dahulu bahwa panjang sisi-sisinya memenuhi aturan tersebut.
Berikut ini adalah beberapa contoh soal lainnya beserta pembahasannya:
Contoh 3: Hitunglah keliling segitiga dengan panjang sisi 7 cm, 9 cm, dan 12 cm.
Penyelesaian:
K = 7 cm + 9 cm + 12 cm
K = 28 cm
Jadi, keliling segitiga dengan panjang sisi 7 cm, 9 cm, dan 12 cm adalah 28 cm.
Contoh 4: Hitunglah keliling segitiga dengan panjang sisi 10 cm, 15 cm, dan 18 cm.
Penyelesaian:
K = 10 cm + 15 cm + 18 cm
K = 43 cm
Sehingga, keliling segitiga dengan panjang sisi 10 cm, 15 cm, dan 18 cm adalah 43 cm.
Bagaimana jika salah satu sisi segitiga tidak diketahui? Dalam kasus ini, dapat digunakan teorema Pythagoras untuk mencari panjang sisi tersebut. Jika segitiga merupakan segitiga sama sisi, maka semua sisinya memiliki panjang yang sama. Jika segitiga sama kaki, maka dua sisinya memiliki panjang yang sama, dan sisinya yang lain lebih pendek. Sedangkan pada segitiga sembarang, semua sisinya memiliki panjang yang berbeda. Berikut ini adalah contoh penggunaan teorema Pythagoras untuk menghitung panjang salah satu sisi segitiga:
Contoh 5: Hitunglah keliling segitiga dengan panjang sisi 5 cm, 12 cm, dan x cm, jika x merupakan panjang sisi miring segitiga siku-siku.
Penyelesaian:
Karena segitiga tersebut merupakan segitiga siku-siku, maka dapat digunakan teorema Pythagoras untuk mencari x:
52 + 122 = x2
x2 = 169
x = 13 cm
Dengan demikian, panjang sisi miring segitiga siku-siku adalah 13 cm, dan keliling segitiga dapat dihitung seperti contoh sebelumnya:
K = 5 cm + 12 cm + 13 cm
K = 30 cm
Jadi, keliling segitiga dengan panjang sisi 5 cm, 12 cm, dan 13 cm adalah 30 cm.
FAQ
1. Apa bedanya antara segitiga sama kaki dan segitiga sama sisi?
Segitiga sama kaki adalah segitiga yang memiliki dua sisi dengan panjang yang sama, sedangkan sisi yang lain lebih pendek. Sedangkan segitiga sama sisi adalah segitiga yang memiliki tiga sisi dengan panjang yang sama. Dalam segitiga sama sisi, semua sudutnya juga memiliki ukuran yang sama.
2. Apa contoh kasus di mana perhitungan luas dan keliling segitiga sering digunakan?
Perhitungan luas dan keliling segitiga sering digunakan dalam pembangunan rumah atau bangunan lainnya, dalam perancangan taman, dalam perhitungan pentingnya benda tertentu, dan dalam berbagai soal matematika di sekolah.