Regresi linier adalah salah satu metode analisis prediksi atau hubungan antara variabel bebas atau variabel yang diukur dengan variabel terikat atau variabel yang akan diperkirakan. Regresi linier sering digunakan untuk menganalisis data pada berbagai macam bidang seperti ekonomi, teknik, dan bisnis. Regresi linier juga dapat digunakan untuk membuat model prediksi yang akan berguna untuk membantu pengambilan keputusan.
Cara Membuat Regresi Linier di Excel
Salah satu aplikasi yang sering digunakan untuk analisis regresi linier adalah Microsoft Excel. Berikut ini adalah langkah-langkah cara membuat regresi linier di Excel:
- Siapkan data yang akan diolah. Data terdiri dari dua variabel, yaitu variabel bebas dan variabel terikat. Variabel bebas biasanya dilambangkan dengan x, sedangkan variabel terikat dilambangkan dengan y.
- Buka aplikasi Microsoft Excel, kemudian buat tabel untuk memasukkan data.
- Pasangkan variabel bebas dan variabel terikat pada tabel yang telah dibuat.
- Pilih data yang akan dihitung, lalu klik tab ‘Insert’ pada menu bar.
- Pilih menu ‘Scatter’, dan pilih ‘Scatter with Straight Lines and Markers’.
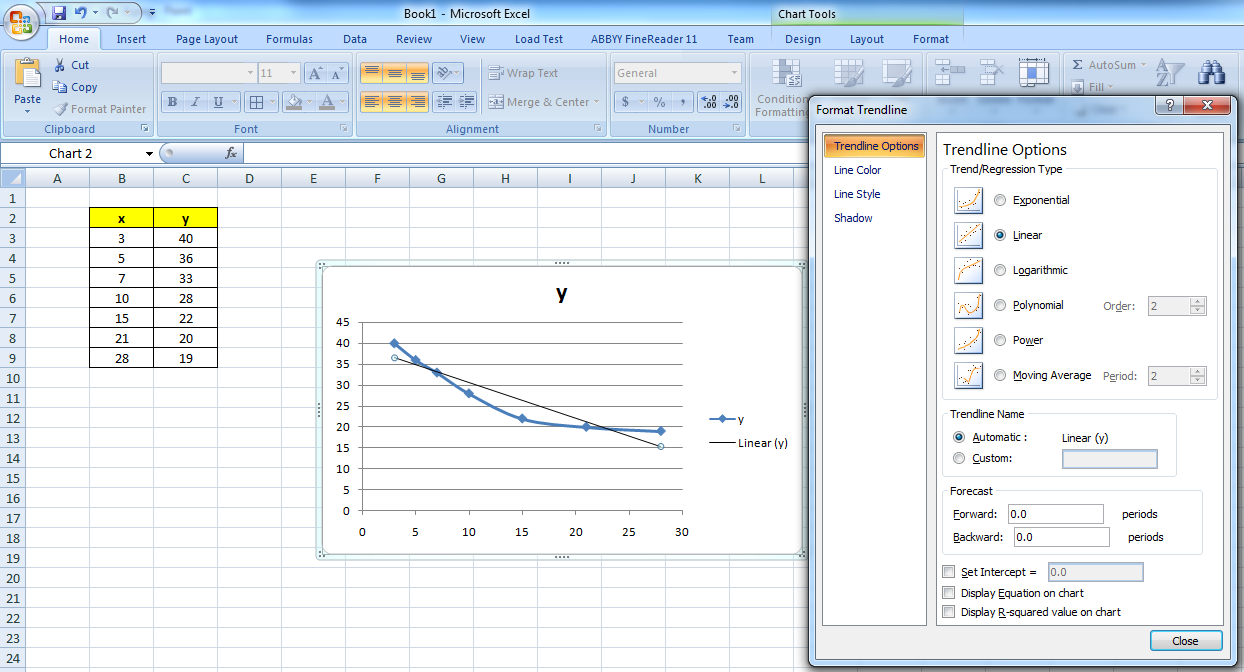
- Lihat grafik yang muncul. Untuk menentukan persamaan regresi linier, klik kanan pada grafik dan pilih ‘Add Trendline’.
- Pada menu ‘Format Trendline’, pilih tab ‘Options’, lalu centang ‘Display Equation on Chart’ dan ‘Display R-squared value on chart’ untuk menampilkan persamaan regresi linier dan nilai R-squared.
Cara Membuat Regresi Linear Sederhana Di Excel Dan Artinya
Regresi linear sederhana adalah metode analisis regresi linier yang digunakan pada dua variabel saja. Berikut ini adalah langkah-langkah cara membuat regresi linear sederhana di Excel:
- Siapkan data yang akan diolah. Data terdiri dari dua variabel, yaitu variabel bebas dan variabel terikat. Variabel bebas biasanya dilambangkan dengan x, sedangkan variabel terikat dilambangkan dengan y.
- Buka aplikasi Microsoft Excel, kemudian buat tabel untuk memasukkan data.
- Pasangkan variabel bebas dan variabel terikat pada tabel yang telah dibuat.
- Pilih data yang akan dihitung, lalu klik tab ‘Insert’ pada menu bar.
- Pilih menu ‘Scatter’, dan pilih ‘Scatter with Straight Lines and Markers’.
- Lihat grafik yang muncul. Untuk menentukan persamaan regresi linier, klik kanan pada grafik dan pilih ‘Add Trendline’.
- Pada menu ‘Format Trendline’, pilih tab ‘Options’, lalu centang ‘Display Equation on Chart’ dan ‘Display R-squared value on chart’ untuk menampilkan persamaan regresi linier dan nilai R-squared.
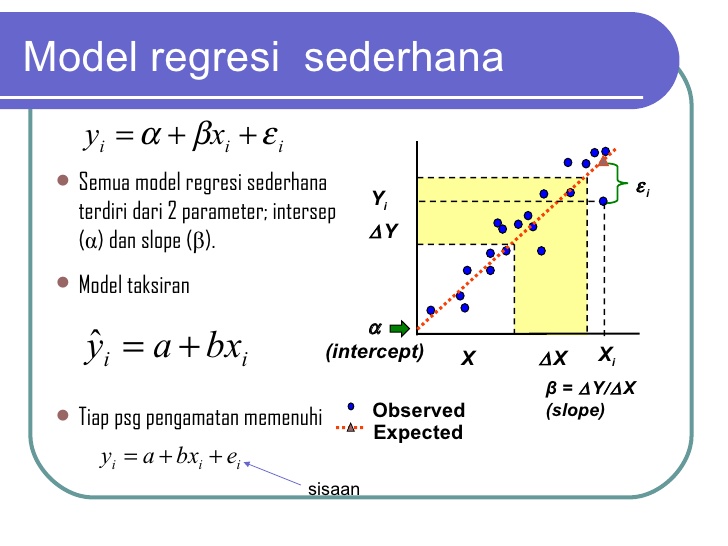
Berikut ini adalah arti dari persamaan regresi linier:
y = a + bx
di mana:
- y adalah variabel terikat
- x adalah variabel bebas
- a adalah perpotongan sumbu y, yaitu titik pada sumbu y di mana garis regresi linier memotongnya. Nilai ini merupakan nilai y ketika x = 0.
- b adalah slope atau kemiringan, yaitu ukuran rate of change antara dua variabel. Nilai ini menunjukkan seberapa banyak kenaikan atau penurunan nilai y saat nilai x bertambah satu satuan. Slope juga menunjukkan arah dari hubungan antara dua variabel. Jika nilai slope positif, maka hubungan antara dua variabel tersebut bersifat positif, sedangkan jika nilai slope negatif maka hubungan antara dua variabel tersebut bersifat negatif.
Analisis Regresi Linear Sederhana (Simple Linear Regression)
Analisis regresi linear sederhana merupakan metode analisis yang digunakan untuk mempelajari hubungan linier antara dua variabel, yaitu variabel bebas (independent variable) dan variabel terikat (dependent variable). Berikut ini adalah contoh analisis regresi linear sederhana:
Sebuah perusahaan ingin mengetahui hubungan antara pendapatan dengan biaya produksi yang dikeluarkan. Data yang dikumpulkan terdiri dari dua variabel, yaitu pendapatan (variabel terikat) dan biaya produksi (variabel bebas). Data ini akan digunakan untuk membuat model prediksi yang dapat membantu perusahaan dalam pengambilan keputusan.
Langkah-langkah analisis regresi linear sederhana adalah sebagai berikut:
- Siapkan data yang akan diolah. Data terdiri dari dua variabel, yaitu variabel bebas dan variabel terikat. Variabel bebas biasanya dilambangkan dengan x, sedangkan variabel terikat dilambangkan dengan y.
- Buat tabel untuk memasukkan data. Siapkan kolom untuk variabel bebas dan terikat.
- Pasangkan variabel bebas dan variabel terikat pada tabel yang telah dibuat.
- Hitung nilai r. Nilai r merupakan koefisien korelasi antara dua variabel. Nilai ini menunjukkan seberapa kuatnya hubungan antara dua variabel. Nilai r dapat dihitung menggunakan rumus:
di mana:
- n adalah jumlah sampel
- X adalah variabel bebas
- Y adalah variabel terikat
Nilai r berkisar antara -1 sampai 1. Jika nilai r positif, maka pertambahan nilai pada variabel bebas akan diikuti oleh pertambahan nilai pada variabel terikat. Jika nilai r negatif, maka pertambahan nilai pada variabel bebas akan diikuti oleh penurunan nilai pada variabel terikat.
Untuk menentukan apakah nilai r signifikan secara statistik, dapat digunakan uji hipotesis. Hipotesis nol adalah tidak ada hubungan antara variabel bebas dan terikat, sedangkan hipotesis alternatif adalah terdapat hubungan antara variabel bebas dan terikat. Jika p-value lebih kecil dari alpha (tingkat signifikansi), maka hipotesis nol ditolak, dan dapat disimpulkan bahwa terdapat hubungan antara variabel bebas dan terikat.
Langkah selanjutnya adalah membangun model prediksi. Model prediksi dapat ditemukan dengan menggunakan persamaan regresi linear sederhana:
di mana:
- y’ adalah nilai terikat yang diprediksi
- b adalah slope atau kemiringan, yaitu ukuran rate of change antara dua variabel. Nilai ini menunjukkan seberapa banyak kenaikan atau penurunan nilai y saat nilai x bertambah satu satuan. Slope juga menunjukkan arah dari hubungan antara dua variabel. Jika nilai slope positif, maka hubungan antara dua variabel tersebut bersifat positif, sedangkan jika nilai slope negatif maka hubungan antara dua variabel tersebut bersifat negatif.
- a adalah perpotongan sumbu y, yaitu titik pada sumbu y di mana garis regresi linier memotongnya. Nilai ini merupakan nilai y ketika x = 0.
- x adalah variabel bebas
FAQ
1. Apakah regresi linear hanya dapat digunakan pada dua variabel saja?
Regresi linear dapat digunakan pada dua variabel atau lebih. Regresi linear yang digunakan untuk tiga atau lebih variabel disebut dengan regresi linear berganda (multiple linear regression).
2. Apa yang menjadi kelebihan menggunakan regresi linier dalam analisis data?
Kelebihan menggunakan regresi linier dalam analisis data adalah:
- Memudahkan kita dalam memahami hubungan antara dua variabel
- Dapat digunakan untuk membuat prediksi
- Dapat digunakan pada berbagai macam bidang, seperti ekonomi, bisnis, dan teknik
- Dapat memperkirakan nilai kuantitatif dari sebuah variabel terikat apabila nilai variabel bebas sudah diketahui